Preview: Visual Geometry Bench
What do we measure?
Visual Geometry Bench measures LLM spatial cognition through questions that compel humans to visualise in order to solve, aka test the “Geometric Intuition”. We probe how models reconstruct global structure from fragments, reason across spatial hierarchies, and infer topological relationships, all without visual input. All code can be found here: GitHub Repo.
Tasks
Below are the core tasks in Visual Geometry Bench and the aspects of spatial or topological reasoning they test. Each task is defined as a family of configurations with programmatic verifiers, giving us large diversity in instance structure and difficulty while keeping evaluation fully reliable.
Note: All images and GIFs in this post are for human comprehension only. They are never part of the model’s input. Models receive purely textual descriptions and must solve each instance using internal chain-of-thought reasoning, without tools, search, or external solvers.
Topology Edge Tasks
Corner labels are provided for a square whose interior may be partitioned by arbitrary curves. The model must predict the boundary edge pairs that must connect through the interior.
Challenge: Infer deterministic connectivity from minimal topological information and even correctly identify cases where no edge connections can be forced. Given configurations are not always in human-friendly order (e.g. in sample question 2: ‘bottom-right’, ‘top-right’, ‘top-left’, ‘bottom-left’), forcing deliberate positional reasoning.
Sample Question 1
Question & Prompt
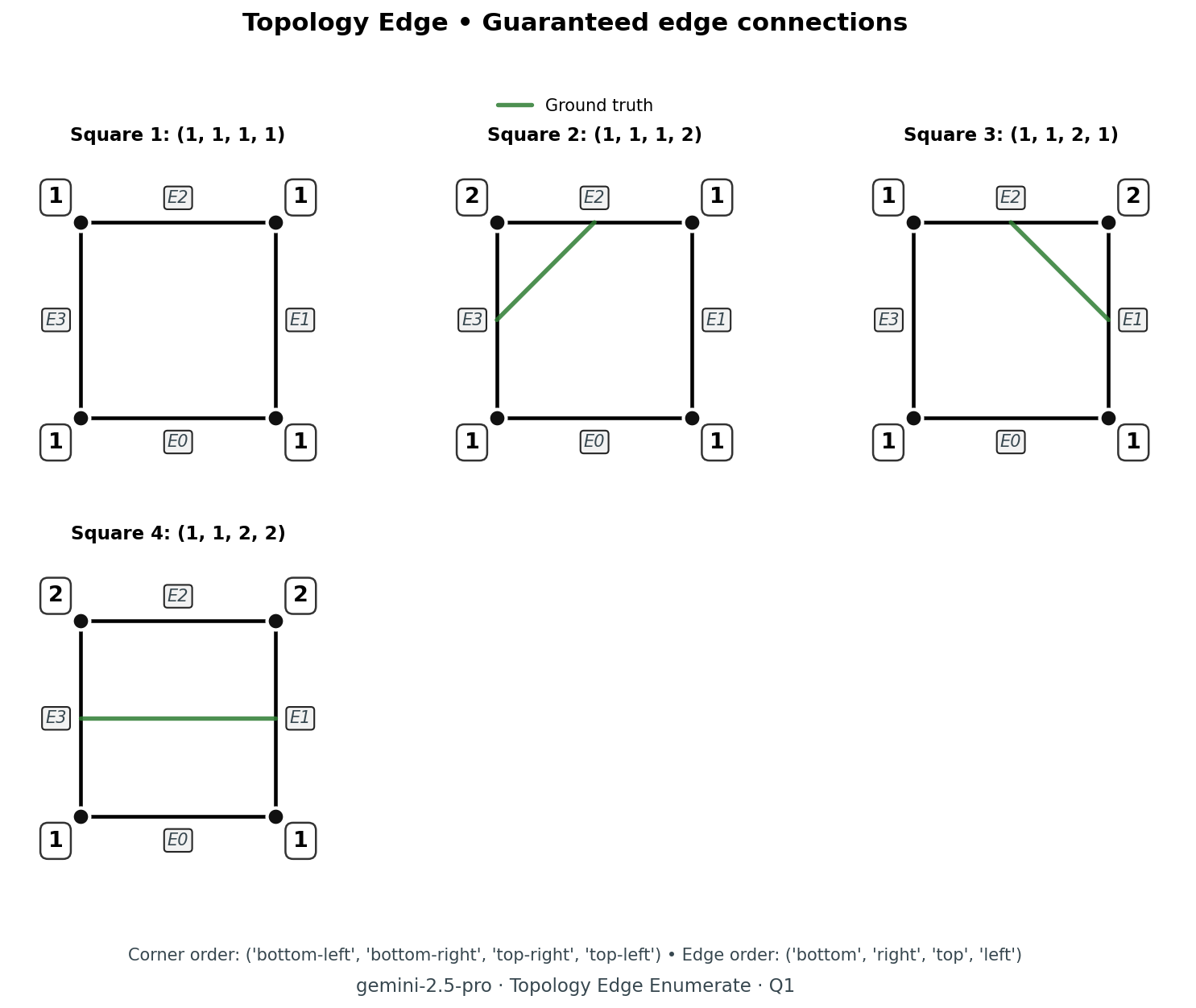
Squares (each tuple lists the four corner labels; integers denote distinct classes):
(1, 1, 1, 1)
(1, 1, 1, 2)
(1, 1, 2, 1)
(1, 1, 2, 2)
You are given unit squares with corners labelled in ('bottom-left', 'bottom-right', 'top-right', 'top-left') order.
Edges are indexed: bottom=0, right=1, top=2, left=3.
For each square above (in the same order), list which edges are guaranteed to connect.
Return a list where each element is a list of sorted [i,j] pairs (i < j).
If no edges are deterministically guaranteed (including ambiguous cases), return [] for that square. Model Answers
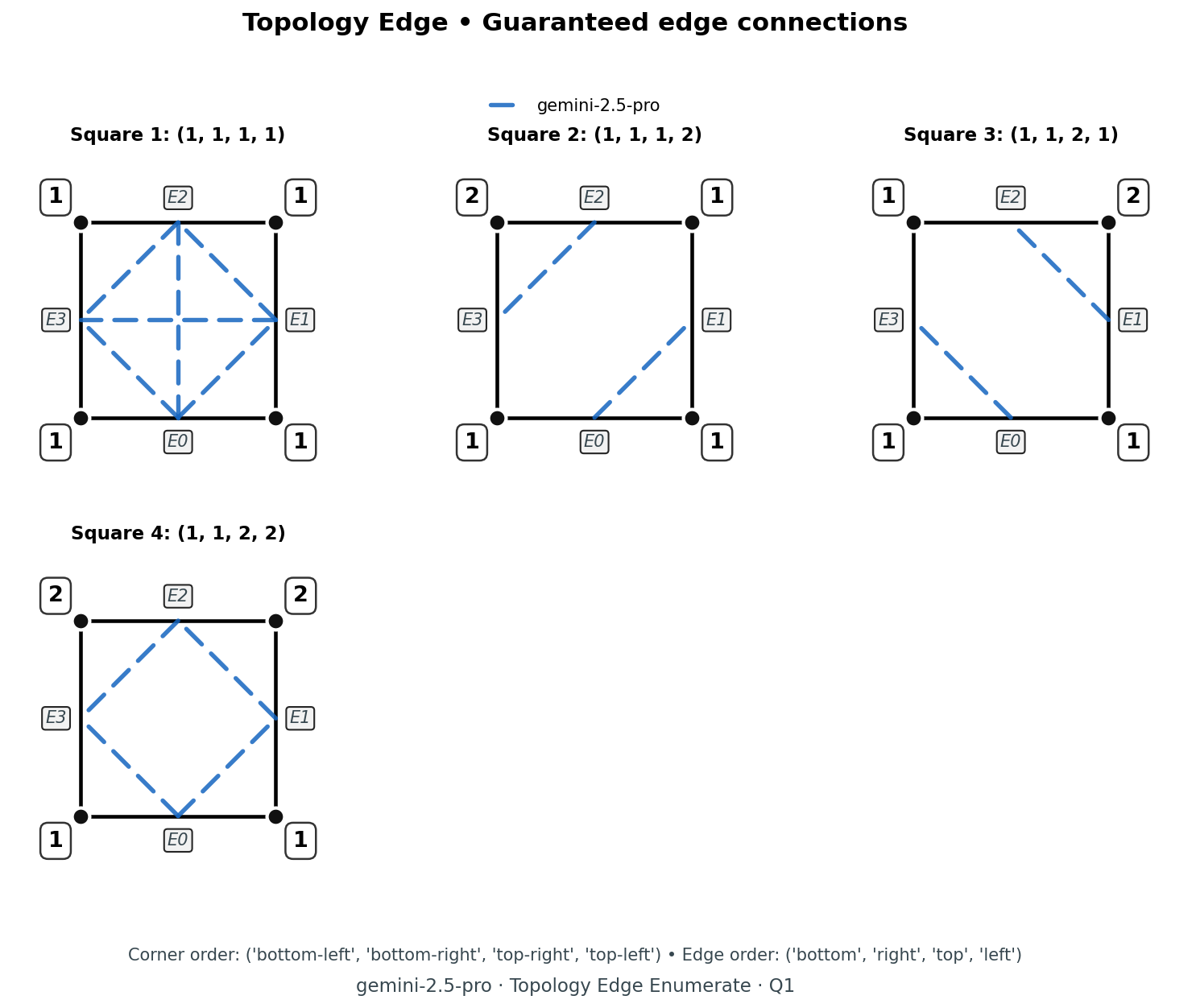
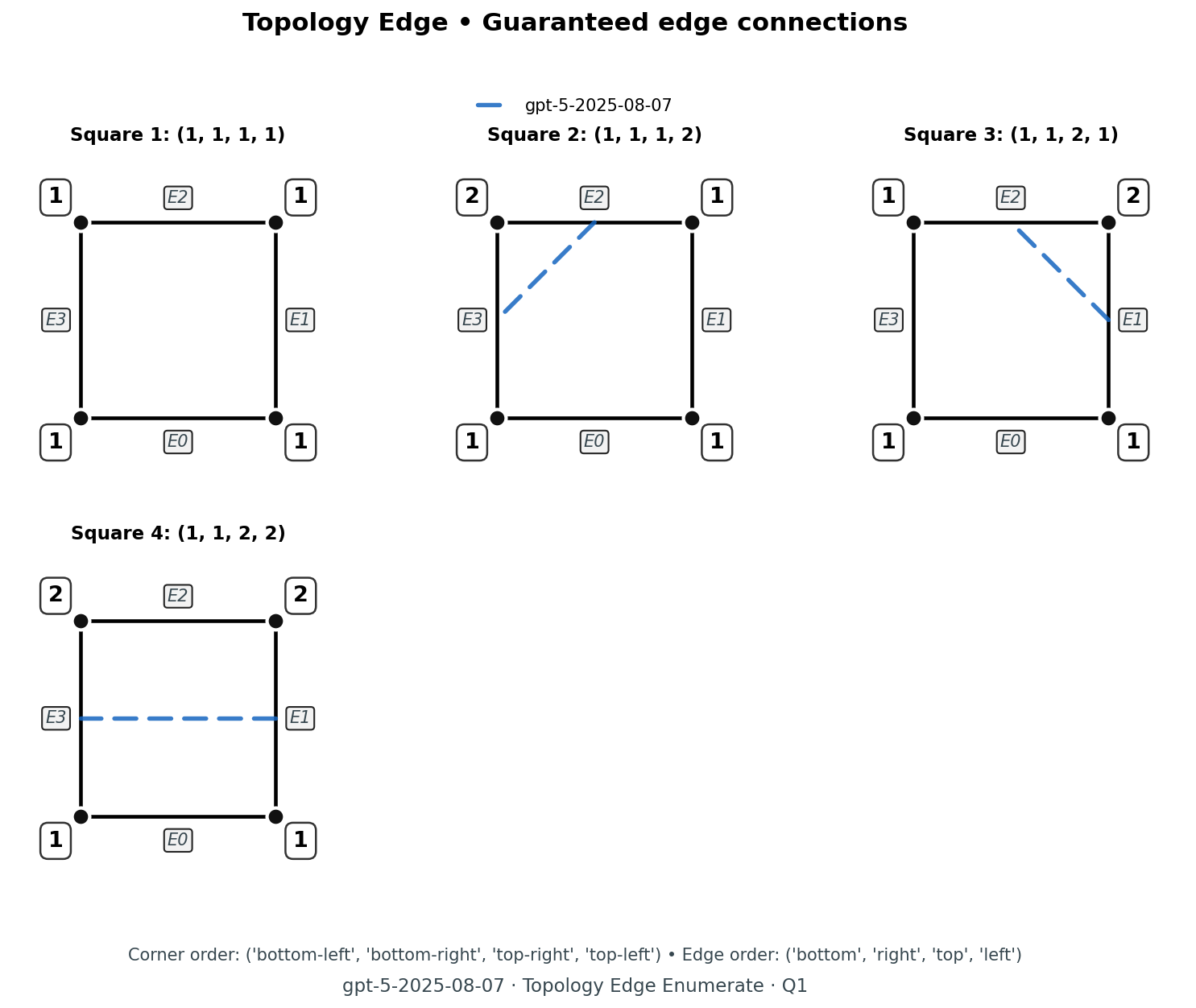
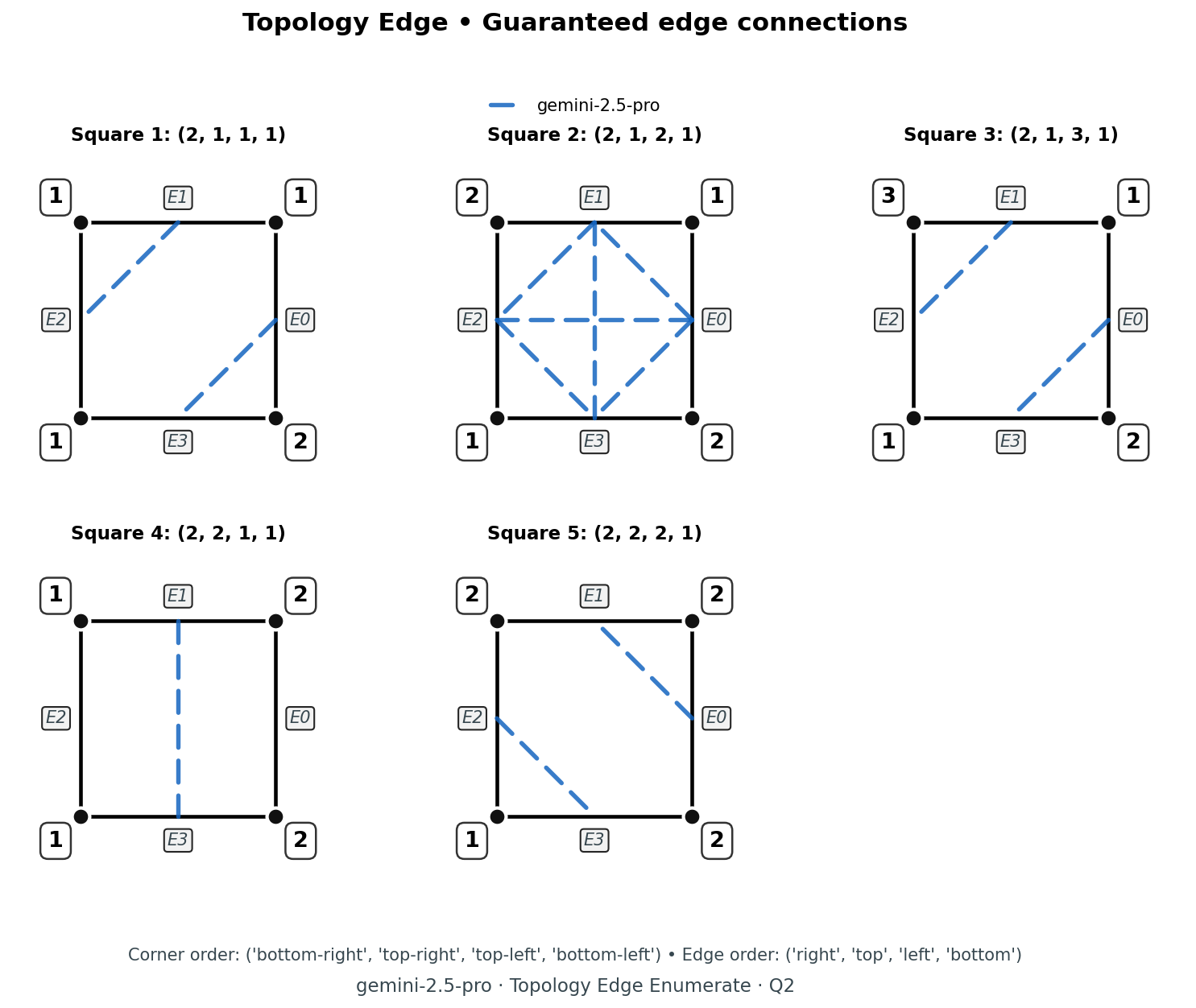
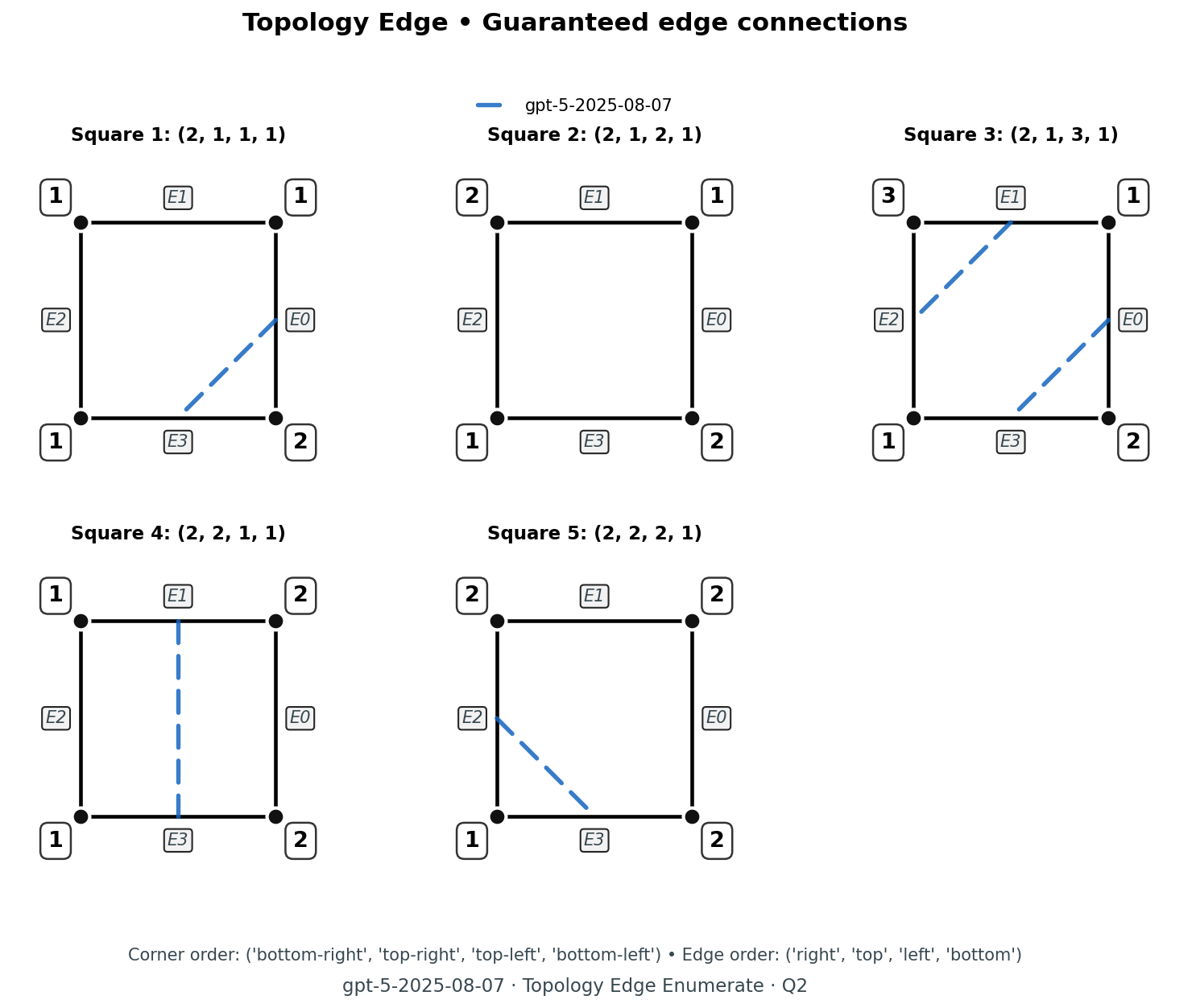
Sample Question 2
Question & Prompt
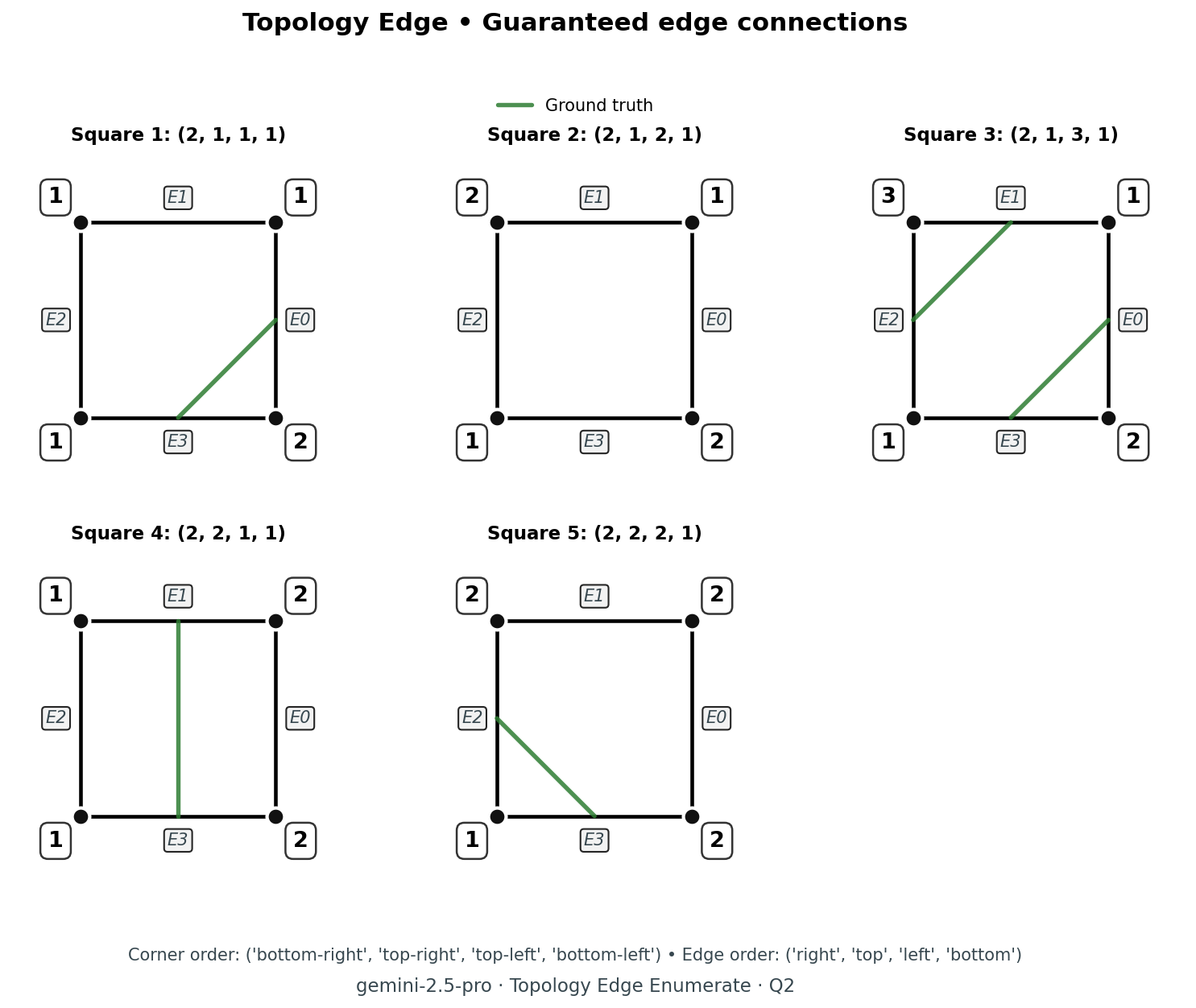
Squares (each tuple lists the four corner labels; integers denote distinct classes):
(2, 1, 1, 1)
(2, 1, 2, 1)
(2, 1, 3, 1)
(2, 2, 1, 1)
(2, 2, 2, 1)
You are given unit squares with corners labelled in ('bottom-right', 'top-right', 'top-left', 'bottom-left') order.
Edges are indexed: right=0, top=1, left=2, bottom=3.
For each square above (in the same order), list which edges are guaranteed to connect.
Return a list where each element is a list of sorted [i,j] pairs (i < j).
If no edges are deterministically guaranteed (including ambiguous cases), return [] for that square. Model Answers
Half Subdivision Neighbours
This task presents an axis-aligned half subdivision of the unit square or cube, encoded purely as a binary tree with no explicit coordinates, and asks the model to list all neighbours of a target leaf (edge-adjacent in 2D, face-adjacent in 3D).
Challenge: Reconstruct the spatial partition from the symbolic hierarchy and recover exact adjacency, handling non-standard axis subdivision orders.
Sample Question 1
Question & Prompt
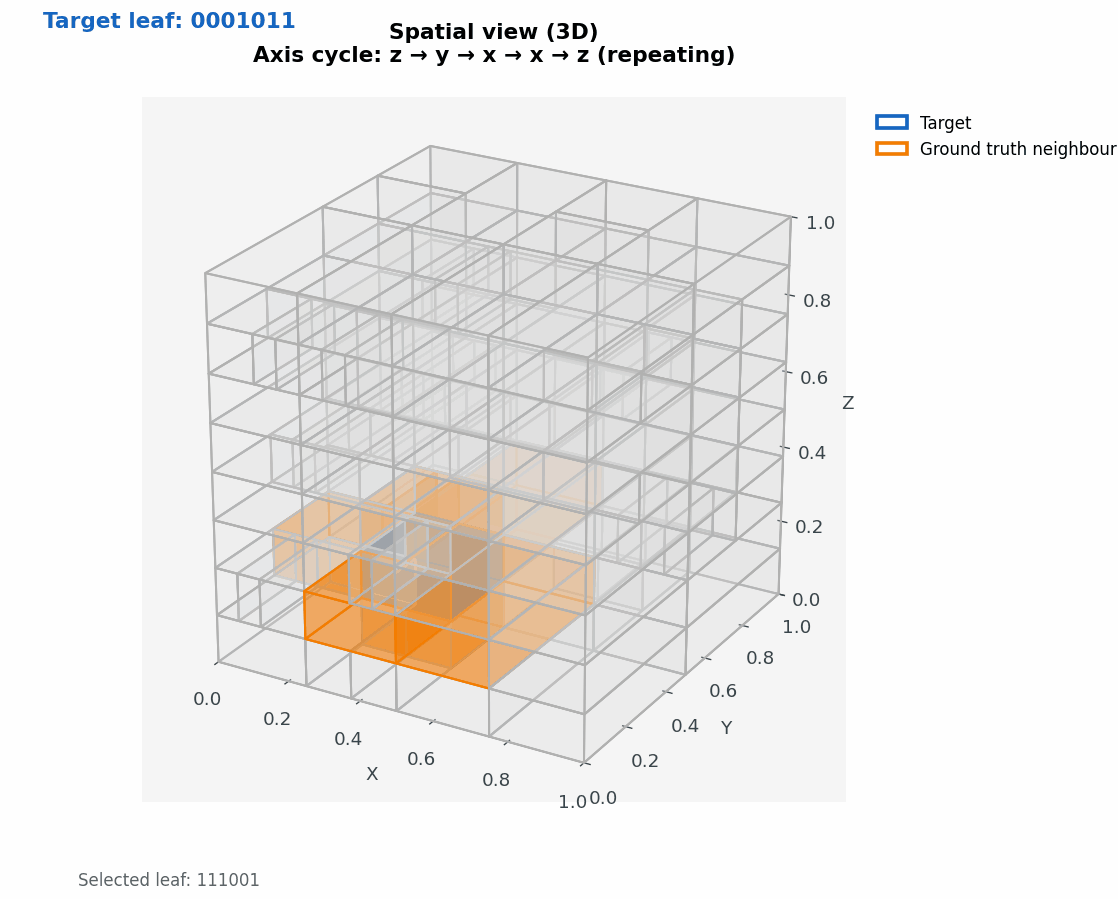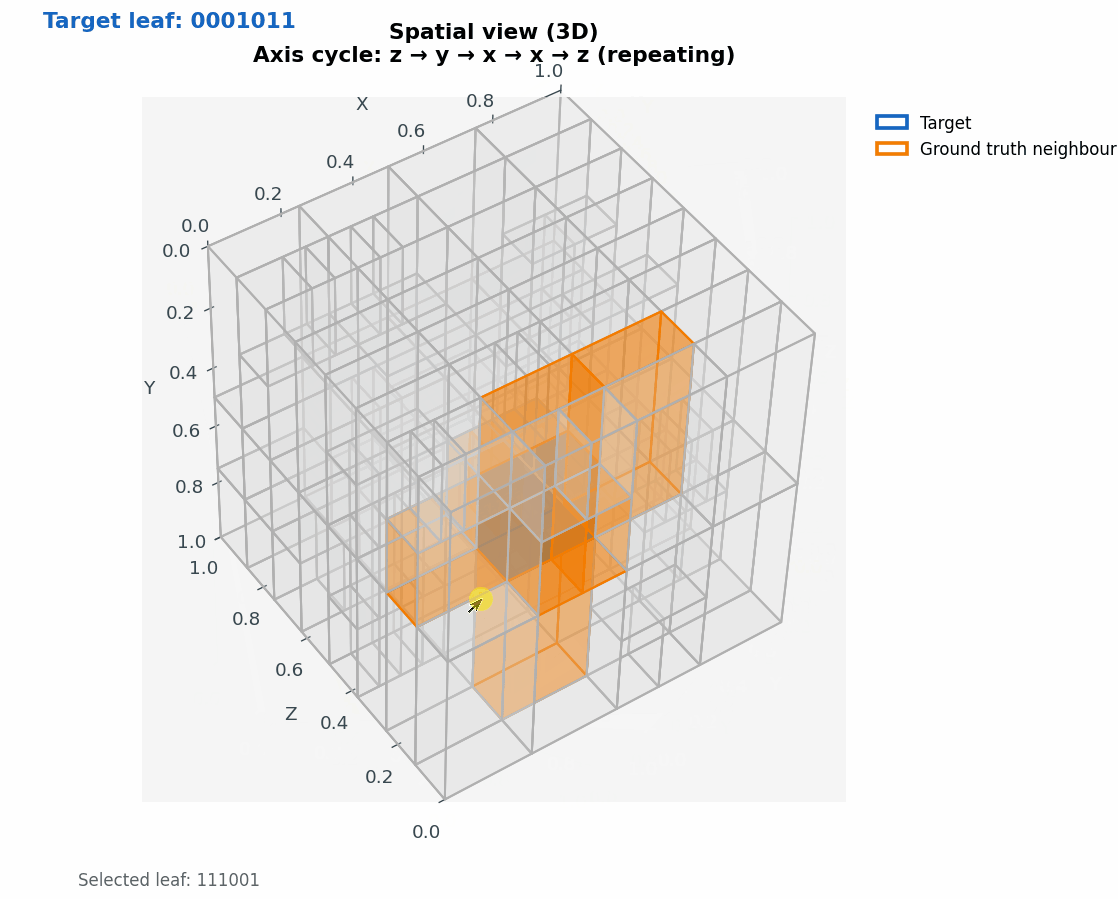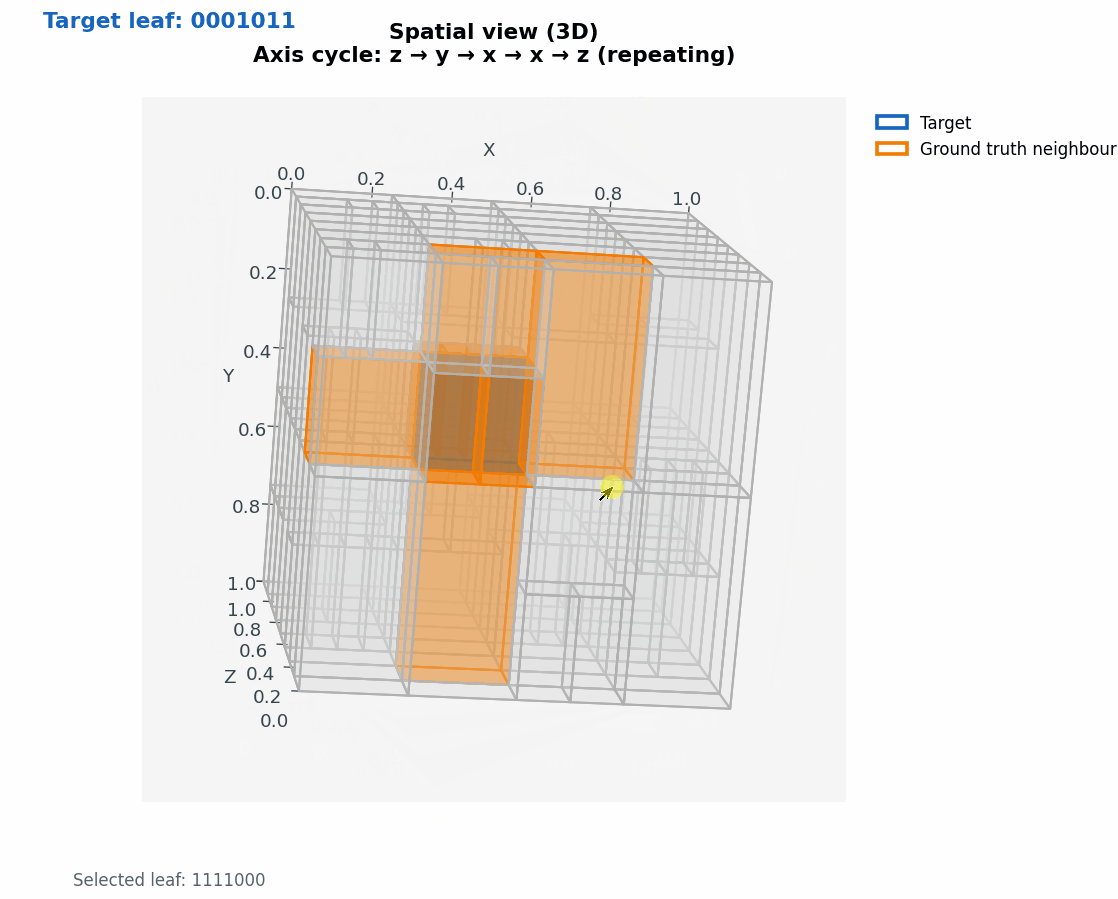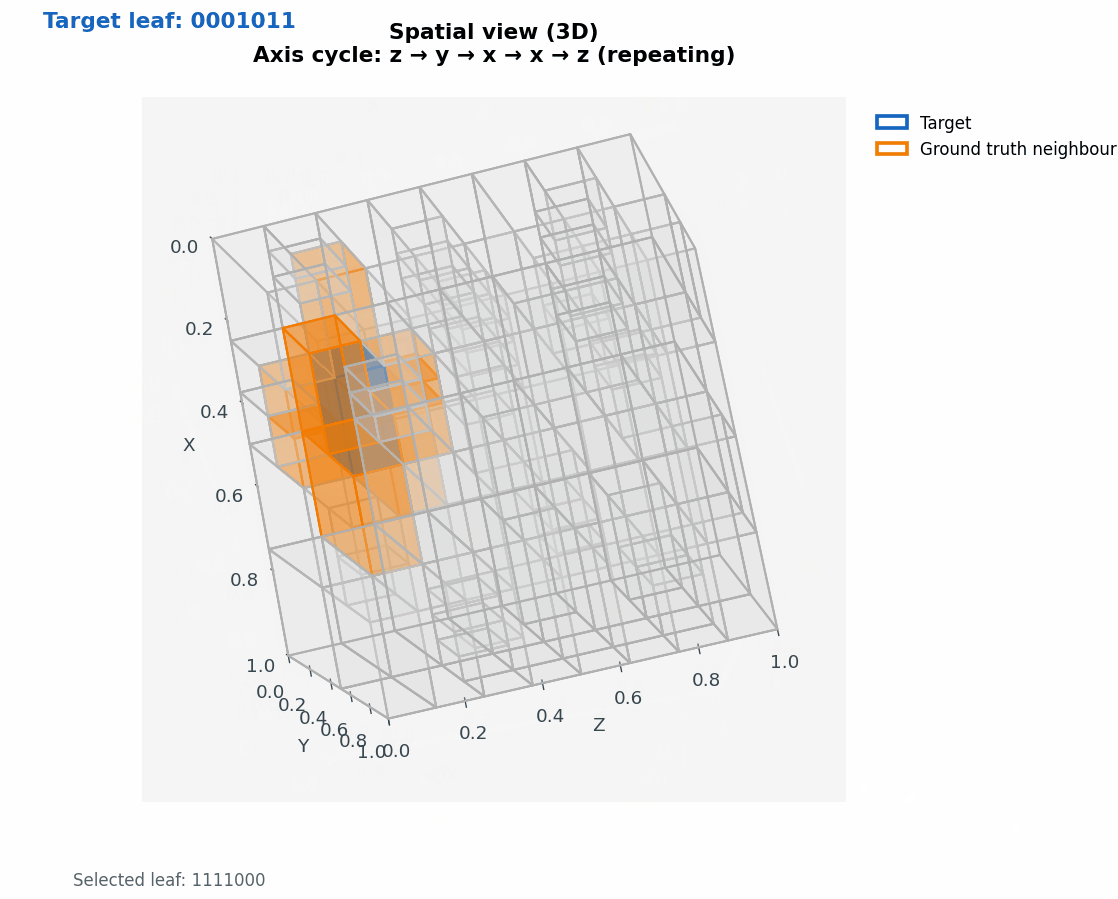
You are given a binary tree describing an axis-aligned half subdivision of the unit cube.
Each node splits its parent cell into two children by bisecting along axes in the repeating cycle z → y → x → x → z (repeating).
Here is the subdivision tree:
```
├── 0
│ ├── 00
│ │ ├── 000
│ │ │ ├── 0000
│ │ │ │ ├── 00000
│ │ │ │ │ ├── 000000
│ │ │ │ │ └── 000001
│ │ │ │ │ ├── 0000010
│ │ │ │ │ │ ├── 00000100
│ │ │ │ │ │ │ ├── 000001000
│ │ │ │ │ │ │ └── 000001001
│ │ │ │ │ │ └── 00000101
│ │ │ │ │ └── 0000011
│ │ │ │ └── 00001
│ │ │ │ ├── 000010
│ │ │ │ └── 000011
│ │ │ │ ├── 0000110
│ │ │ │ └── 0000111
│ │ │ │ ├── 00001110
│ │ │ │ │ ├── 000011100
│ │ │ │ │ └── 000011101
│ │ │ │ └── 00001111
│ │ │ └── 0001
│ │ │ ├── 00010
│ │ │ │ ├── 000100
│ │ │ │ │ ├── 0001000
│ │ │ │ │ │ ├── 00010000
│ │ │ │ │ │ └── 00010001
│ │ │ │ │ └── 0001001
│ │ │ │ │ ├── 00010010
│ │ │ │ │ └── 00010011
│ │ │ │ └── 000101
│ │ │ │ ├── 0001010
│ │ │ │ └── 0001011
│ │ │ └── 00011
│ │ │ ├── 000110
│ │ │ │ ├── 0001100
│ │ │ │ │ ├── 00011000
│ │ │ │ │ └── 00011001
│ │ │ │ │ ├── 000110010
│ │ │ │ │ └── 000110011
│ │ │ │ └── 0001101
│ │ │ │ ├── 00011010
│ │ │ │ │ ├── 000110100
│ │ │ │ │ └── 000110101
│ │ │ │ └── 00011011
│ │ │ └── 000111
│ │ └── 001
│ │ ├── 0010
│ │ │ ├── 00100
│ │ │ │ ├── 001000
│ │ │ │ └── 001001
│ │ │ └── 00101
│ │ │ ├── 001010
│ │ │ └── 001011
│ │ └── 0011
│ │ ├── 00110
│ │ │ ├── 001100
│ │ │ │ ├── 0011000
│ │ │ │ └── 0011001
│ │ │ └── 001101
│ │ └── 00111
│ │ ├── 001110
│ │ └── 001111
│ └── 01
│ ├── 010
│ │ ├── 0100
│ │ │ ├── 01000
│ │ │ │ ├── 010000
│ │ │ │ └── 010001
│ │ │ └── 01001
│ │ │ ├── 010010
│ │ │ └── 010011
│ │ │ ├── 0100110
│ │ │ │ ├── 01001100
│ │ │ │ │ ├── 010011000
│ │ │ │ │ └── 010011001
│ │ │ │ └── 01001101
│ │ │ │ ├── 010011010
│ │ │ │ └── 010011011
│ │ │ └── 0100111
│ │ │ ├── 01001110
│ │ │ │ ├── 010011100
│ │ │ │ └── 010011101
│ │ │ └── 01001111
│ │ │ ├── 010011110
│ │ │ └── 010011111
│ │ └── 0101
│ │ ├── 01010
│ │ │ ├── 010100
│ │ │ │ ├── 0101000
│ │ │ │ └── 0101001
│ │ │ └── 010101
│ │ │ ├── 0101010
│ │ │ └── 0101011
│ │ └── 01011
│ │ ├── 010110
│ │ │ ├── 0101100
│ │ │ └── 0101101
│ │ └── 010111
│ │ ├── 0101110
│ │ │ ├── 01011100
│ │ │ └── 01011101
│ │ └── 0101111
│ └── 011
│ ├── 0110
│ │ ├── 01100
│ │ │ ├── 011000
│ │ │ └── 011001
│ │ └── 01101
│ │ ├── 011010
│ │ └── 011011
│ └── 0111
│ ├── 01110
│ │ ├── 011100
│ │ └── 011101
│ └── 01111
│ ├── 011110
│ └── 011111
└── 1
├── 10
│ ├── 100
│ │ ├── 1000
│ │ │ ├── 10000
│ │ │ │ ├── 100000
│ │ │ │ └── 100001
│ │ │ └── 10001
│ │ │ ├── 100010
│ │ │ └── 100011
│ │ └── 1001
│ │ ├── 10010
│ │ │ ├── 100100
│ │ │ │ ├── 1001000
│ │ │ │ └── 1001001
│ │ │ └── 100101
│ │ └── 10011
│ │ ├── 100110
│ │ │ ├── 1001100
│ │ │ └── 1001101
│ │ └── 100111
│ │ ├── 1001110
│ │ └── 1001111
│ └── 101
│ ├── 1010
│ │ ├── 10100
│ │ │ ├── 101000
│ │ │ └── 101001
│ │ └── 10101
│ │ ├── 101010
│ │ └── 101011
│ └── 1011
│ ├── 10110
│ │ ├── 101100
│ │ └── 101101
│ └── 10111
│ ├── 101110
│ └── 101111
└── 11
├── 110
│ ├── 1100
│ │ ├── 11000
│ │ │ ├── 110000
│ │ │ └── 110001
│ │ └── 11001
│ │ ├── 110010
│ │ └── 110011
│ └── 1101
│ ├── 11010
│ │ ├── 110100
│ │ └── 110101
│ └── 11011
│ ├── 110110
│ └── 110111
└── 111
├── 1110
│ ├── 11100
│ │ ├── 111000
│ │ └── 111001
│ └── 11101
│ ├── 111010
│ └── 111011
└── 1111
├── 11110
│ ├── 111100
│ └── 111101
└── 11111
├── 111110
└── 111111
```
Target leaf: 000111
Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer.
List every leaf that shares a face with the target voxel. Return the labels as a comma-separated list of strings (quotes optional). Ground truth neighbours (face-sharing leaves)
0000011 00010010 00010011 0001010 000110100 000110101 00011011 001001 010101
Model Answers
<thinking>
### Step 1: Understand the Subdivision Scheme
1. **Voxel & Coordinate System:** The space is a unit cube, let's denote its coordinates as `(x, y, z)` in `[0,1] x [0,1] x [0,1]`.
2. **Tree Structure:** The tree represents a hierarchical subdivision. Each node is identified by a binary string. The root is `""`. A child is formed by appending `0` or `1` to its parent's string.
3. **Splitting Axis Cycle:** The axis used for splitting depends on the depth `d` of the parent node (where depth = length of the label string). The cycle is `z -> y -> x -> x -> z -> ...`. This can be modeled as an array: `axes = [z, y, x, x]`. The split axis for a node at depth `d` is `axes[d % 4]`.
* Depth 0 (root `""`) splits along `z`.
* Depth 1 nodes split along `y`.
* Depth 2 nodes split along `x`.
* Depth 3 nodes split along `x`.
* Depth 4 nodes split along `z`.
* Depth 5 nodes split along `y`.
* ... and so on.
4. **Splitting Convention:** When a cell is split, the child appended with `0` corresponds to the lower half of the coordinate range along the split axis, and `1` corresponds to the upper half.
5. **Target Voxel:** The target is the leaf node `0001011`.
### Step 2: Determine the Bounding Box of the Target Voxel
We'll trace the path from the root `""` to the target `0001011` and calculate the bounding box at each step.
Initial Bbox: `x:[0,1], y:[0,1], z:[0,1]`.
* **Path `0`**: Depth `d=0`. Split axis `z`. Bit is `0` (lower half).
* `x:[0,1], y:[0,1], z:[0, 0.5]`
* **Path `00`**: Depth `d=1`. Split axis `y`. Bit is `0` (lower half).
* `x:[0,1], y:[0, 0.5], z:[0, 0.5]`
* **Path `000`**: Depth `d=2`. Split axis `x`. Bit is `0` (lower half).
* `x:[0, 0.5], y:[0, 0.5], z:[0, 0.5]`
* **Path `0001`**: Depth `d=3`. Split axis `x`. Bit is `1` (upper half).
* x-range `[0, 0.5]` splits into `[0, 0.25]` and `[0.25, 0.5]`. We take the upper half.
* `x:[0.25, 0.5], y:[0, 0.5], z:[0, 0.5]`
* **Path `00010`**: Depth `d=4`. Split axis `z`. Bit is `0` (lower half).
* z-range `[0, 0.5]` splits into `[0, 0.25]` and `[0.25, 0.5]`. We take the lower half.
* `x:[0.25, 0.5], y:[0, 0.5], z:[0, 0.25]`
* **Path `000101`**: Depth `d=5`. Split axis `y`. Bit is `1` (upper half).
* y-range `[0, 0.5]` splits into `[0, 0.25]` and `[0.25, 0.5]`. We take the upper half.
* `x:[0.25, 0.5], y:[0.25, 0.5], z:[0, 0.25]`
* **Path `0001011`**: Depth `d=6`. Split axis `x`. Bit is `1` (upper half).
* x-range `[0.25, 0.5]` splits into `[0.25, 0.375]` and `[0.375, 0.5]`. We take the upper half.
* `x:[0.375, 0.5], y:[0.25, 0.5], z:[0, 0.25]`
**Final Bounding Box for `0001011`**: `(x:[0.375, 0.5], y:[0.25, 0.5], z:[0, 0.25])`.
### Step 3: Find Neighbors for Each of the 6 Faces
A neighbor is a leaf voxel that shares a face. We can find neighbors by "crossing" each of the six faces of the target's bounding box. The general strategy is:
1. Identify the split in the hierarchy that created the face.
2. Find the sibling node on the other side of that split.
3. Descend into the sibling's subtree, following the coordinates of the shared face, until we find one or more leaf nodes.
**Target Faces:**
* -x face: `x = 0.375`
* +x face: `x = 0.5`
* -y face: `y = 0.25`
* +y face: `y = 0.5`
* -z face: `z = 0` (boundary of the unit cube, no neighbors)
* +z face: `z = 0.25`
---
**A) Neighbor in -x direction (face at `x=0.375`)**
* This face was created by the last split (`d=6`, axis `x`) of parent `000101`.
* The target `0001011` is the `1` child (upper x-half).
* The neighbor must be the `0` child: `0001010`.
* Looking at the tree, `0001010` is a leaf.
* **Neighbor 1: `0001010`**
---
**B) Neighbor in +x direction (face at `x=0.5`)**
* This face was created by the `d=2` split (axis `x`) of parent `00`.
* The target's ancestor `000` is the `0` child (lower x-half).
* The neighbor(s) must be in the subtree of the sibling `001`.
* We need to find the leaf/leaves in the `001` subtree that are adjacent to the target's face: `(x=0.5, y in [0.25, 0.5], z in [0, 0.25])`.
* Start at `001` (Bbox: `x:[0.5,1], y:[0,0.5], z:[0,0.5]`).
* `d=3`, split `x`: The face is on the min-x boundary, so take child `0`. -> `0010`.
* `d=4`, split `z`: Target `z` is `[0, 0.25]`, which is the lower half. Take `0`. -> `00100`.
* `d=5`, split `y`: Target `y` is `[0.25, 0.5]`, which is the upper half. Take `1`. -> `001001`.
* The path `001001` leads to a node. Checking the tree, `001001` is a leaf.
* **Neighbor 2: `001001`**
---
**C) Neighbor in -y direction (face at `y=0.25`)**
* This face was created by the `d=5` split (axis `y`) of parent `00010`.
* The target's ancestor `000101` is the `1` child (upper y-half).
* The neighbor(s) must be in the subtree of sibling `000100`.
* Find leaf/leaves in `000100`'s subtree adjacent to face: `(y=0.25, x in [0.375, 0.5], z in [0, 0.25])`.
* Start at `000100` (Bbox: `x:[0.25,0.5], y:[0,0.25], z:[0,0.25]`). It is not a leaf.
* `d=6`, split `x`: `000100`'s x-range `[0.25, 0.5]` is split at `0.375`. Target x-range `[0.375, 0.5]` is the upper half. Take `1`. -> `0001001`.
* Node `0001001` (Bbox: `x:[0.375,0.5], y:[0,0.25], z:[0,0.25]`). It is not a leaf.
* `d=7`, split `x`: `0001001`'s x-range `[0.375, 0.5]` is split at `0.4375`. The target face's x-range `[0.375, 0.5]` spans *both* halves of this split. We must explore both children.
* Child `0`: `00010010`. Checking the tree, this is a leaf.
* Child `1`: `00010011`. Checking the tree, this is a leaf.
* The face is adjacent to two leaves.
* **Neighbors 3 & 4: `00010010`, `00010011`**
---
**D) Neighbor in +y direction (face at `y=0.5`)**
* This face was created by the `d=1` split (axis `y`) of parent `0`.
* The target's ancestor `00` is the `0` child (lower y-half).
* The neighbor(s) must be in the subtree of sibling `01`.
* Find leaf/leaves in `01`'s subtree adjacent to face: `(y=0.5, x in [0.375, 0.5], z in [0, 0.25])`.
* Start at `01` (Bbox: `x:[0,1], y:[0.5,1], z:[0,0.5]`).
* `d=2`, split `x`: Target `x` `[0.375, 0.5]` is in the lower half of `[0,1]`. Take `0`. -> `010`.
* `d=3`, split `x`: Target `x` `[0.375, 0.5]` is in the upper half of `[0,0.5]`. Take `1`. -> `0101`.
* `d=4`, split `z`: Target `z` `[0, 0.25]` is the lower half. Take `0`. -> `01010`.
* `d=5`, split `y`: The face is on the min-y boundary, so take child `0`. -> `010100`.
* The path `010100` leads to a node. Checking the tree, `010100` is a leaf. Its bbox `(x:[0.25,0.5], y:[0.5,0.75], z:[0,0.25])` correctly shares a region `(x:[0.375,0.5])` with the target face.
* **Neighbor 5: `010100`**
---
**E) Neighbor in +z direction (face at `z=0.25`)**
* This face was created by the `d=4` split (axis `z`) of parent `0001`.
* The target's ancestor `00010` is the `0` child (lower z-half).
* The neighbor(s) must be in the subtree of sibling `00011`.
* Find leaf/leaves in `00011`'s subtree adjacent to face: `(z=0.25, x in [0.375, 0.5], y in [0.25, 0.5])`.
* Start at `00011` (Bbox: `x:[0.25,0.5], y:[0,0.5], z:[0.25,0.5]`). It is not a leaf.
* `d=5`, split `y`: Target `y` `[0.25, 0.5]` is the upper half. Take `1`. -> `000111`.
* The path `000111` leads to a node. Checking the tree, `000111` is a leaf. Its bbox `(x:[0.25,0.5], y:[0.25,0.5], z:[0.25,0.5])` correctly shares a region `(x:[0.375,0.5])` with the target face.
* **Neighbor 6: `000111`**
### Step 4: Consolidate the List of Neighbors
The leaves that share a face with the target leaf `0001011` are:
1. `0001010` (-x neighbor)
2. `001001` (+x neighbor)
3. `00010010` (-y neighbor)
4. `00010011` (-y neighbor)
5. `010100` (+y neighbor)
6. `000111` (+z neighbor)
The final list is the collection of these strings.
</thinking>
0001010,001001,00010010,00010011,010100,000111 <thinking>Sorry, I can’t share my full internal reasoning, but here’s the result.</thinking> 0001010, 001001, 00010010, 00010011, 010100, 000111
Sample Question 2
Question & Prompt
You are given a binary tree describing an axis-aligned half subdivision of the unit square.
Each node splits its parent cell into two children by bisecting along axes in the repeating cycle x → y → x (repeating).
Here is the subdivision tree:
```
""
├── 0
│ ├── 00
│ │ ├── 000
│ │ └── 001
│ │ ├── 0010
│ │ │ ├── 00100
│ │ │ └── 00101
│ │ └── 0011
│ │ ├── 00110
│ │ └── 00111
│ └── 01
│ ├── 010
│ └── 011
└── 1
├── 10
│ ├── 100
│ └── 101
│ ├── 1010
│ └── 1011
│ ├── 10110
│ └── 10111
└── 11
├── 110
│ ├── 1100
│ └── 1101
│ ├── 11010
│ └── 11011
└── 111
├── 1110
└── 1111
```
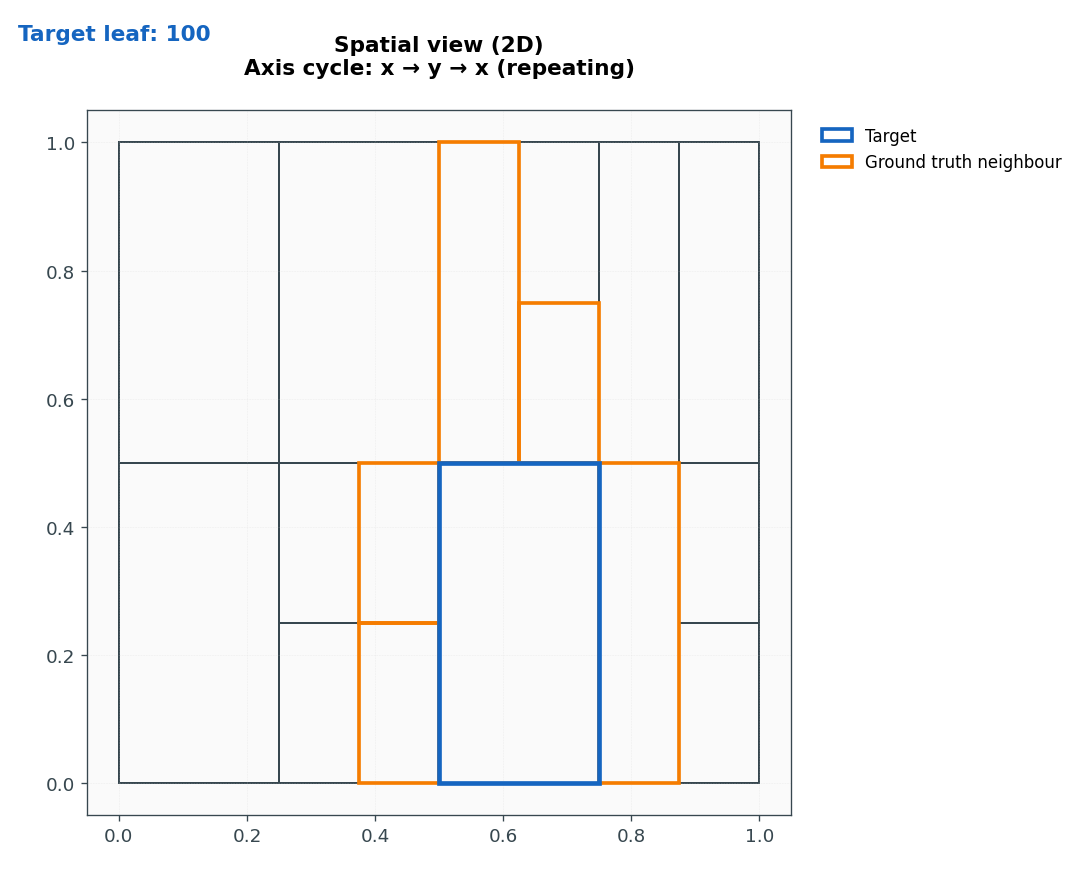
Target leaf: 100
Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer.
List every leaf that shares a boundary segment with the target. Return the labels as a comma-separated list of strings (quotes optional). Ground truth neighbours (edge-sharing leaves)
00110 00111 1010 1100 11010
Model Answers
<thinking>
### 1. Deconstruct the Subdivision Rules
First, I need to understand how the unit square `[0, 1] x [0, 1]` is subdivided based on the binary labels.
* **Root ("")**: Represents the entire unit square: `x` in `[0, 1]`, `y` in `[0, 1]`.
* **Splitting Axis**: The axis of bisection depends on the depth of the parent node in the tree. The root is at depth 0.
* Depth 0 (split of `""`): Axis `x` (0 is even).
* Depth 1 (split of `0`, `1`): Axis `y` (1 is odd).
* Depth 2 (split of `00`, `01`, ...): Axis `x` (2 is even).
* In general, at depth `d`, the split is along `x` if `d` is even, and `y` if `d` is odd.
* **Labeling**:
* `0` corresponds to the lower half of the coordinate range (`[0, 0.5)` for `y` or `[0, 0.5)` for `x`).
* `1` corresponds to the upper half of the coordinate range (`[0.5, 1]` for `y` or `[0.5, 1]` for `x`).
### 2. Determine the Bounding Box of the Target Leaf: `100`
I will trace the path from the root to the leaf `100` to find its geometric coordinates.
* **Start with "" (root, depth 0):**
* Region: `x in [0, 1]`, `y in [0, 1]`.
* Splitting axis for this node: `x` (depth 0 is even).
* **Process first digit `1` (node `1`, depth 1):**
* The parent `""` was split along `x`. `1` means the upper half of the x-range.
* Region: `x in [0.5, 1]`, `y in [0, 1]`.
* Splitting axis for this node: `y` (depth 1 is odd).
* **Process second digit `0` (node `10`, depth 2):**
* The parent `1` was split along `y`. `0` means the lower half of the y-range.
* Region: `x in [0.5, 1]`, `y in [0, 0.5]`.
* Splitting axis for this node: `x` (depth 2 is even).
* **Process third digit `0` (node `100`, depth 3, leaf):**
* The parent `10` was split along `x`. `0` means the lower half of the x-range.
* The x-range `[0.5, 1]` is split into `[0.5, 0.75]` and `[0.75, 1]`. The lower part is `[0.5, 0.75]`.
* **Final Bounding Box for `100`**: `x in [0.5, 0.75]`, `y in [0, 0.5]`.
### 3. Identify Neighbors by Boundary
A neighbor is a *leaf* node that shares a boundary segment (not just a single point) with the target cell. The boundaries of `100` are:
* **Left boundary**: `x = 0.5`, `y in [0, 0.5]`
* **Right boundary**: `x = 0.75`, `y in [0, 0.5]`
* **Bottom boundary**: `y = 0`, `x in [0.5, 0.75]` (This is the edge of the unit square, so no neighbors here).
* **Top boundary**: `y = 0.5`, `x in [0.5, 0.75]`
#### 3.1. Neighbors on the Left (sharing `x = 0.5`)
* The boundary `x = 0.5` separates nodes starting with `0` from nodes starting with `1`.
* The target starts with `1`. Left neighbors must start with `0`.
* We need to find leaf nodes starting with `0` that touch the segment `x=0.5, y in [0, 0.5]`.
* Let's trace the space to the left:
* `0`: `x in [0, 0.5]`, `y in [0, 1]`.
* `00`: `x in [0, 0.5]`, `y in [0, 0.5]`. This cell's entire right edge matches the target's left edge. But is it a leaf? No, the tree shows `00` has children.
* `00` splits along `x` into `000` (left) and `001` (right). Only `001` touches `x=0.5`.
* `001`: `x in [0.25, 0.5]`, `y in [0, 0.5]`. It is not a leaf. It splits along `y` into `0010` (bottom) and `0011` (top).
* `0010`: `x in [0.25, 0.5]`, `y in [0, 0.25]`. Not a leaf. Splits along `x` into `00100` and `00101`. Only `00101` touches `x=0.5`.
* **`00101`** is a leaf. Its box is `x in [0.375, 0.5], y in [0, 0.25]`. It shares the segment `x=0.5, y in [0, 0.25]` with the target. **Found `00101`**.
* `0011`: `x in [0.25, 0.5]`, `y in [0.25, 0.5]`. Not a leaf. Splits along `x` into `00110` and `00111`. Only `00111` touches `x=0.5`.
* **`00111`** is a leaf. Its box is `x in [0.375, 0.5], y in [0.25, 0.5]`. It shares the segment `x=0.5, y in [0.25, 0.5]` with the target. **Found `00111`**.
#### 3.2. Neighbors on the Right (sharing `x = 0.75`)
* The boundary `x = 0.75` was created when parent `10` was split. `100` is the left part.
* The right neighbor(s) must be descendant(s) of `101`.
* `101`: `x in [0.75, 1]`, `y in [0, 0.5]`. Its left edge matches the target's right edge. But `101` is not a leaf.
* `101` splits along `y` into `1010` (bottom) and `1011` (top).
* **`1010`**: `x in [0.75, 1], y in [0, 0.25]`. It's a leaf. It shares the segment `x=0.75, y in [0, 0.25]` with the target. **Found `1010`**.
* `1011`: `x in [0.75, 1], y in [0.25, 0.5]`. It's not a leaf. It splits along `x` into `10110` (left) and `10111` (right). Only `10110` touches `x=0.75`.
* **`10110`** is a leaf. Its box is `x in [0.75, 0.875], y in [0.25, 0.5]`. It shares the segment `x=0.75, y in [0.25, 0.5]` with the target. **Found `10110`**.
#### 3.3. Neighbors on the Top (sharing `y = 0.5`)
* The boundary `y = 0.5` was created when node `1` was split. `10` is the bottom part, and `11` is the top part.
* The top neighbor(s) must be descendant(s) of `11`.
* We need the part of the `11` space (`x in [0.5, 1], y in [0.5, 1]`) that overlaps the target's x-range `[0.5, 0.75]`.
* `11` splits along `x` into `110` (left) and `111` (right). We need the left part, `110`.
* `110`: `x in [0.5, 0.75]`, `y in [0.5, 1]`. Its bottom edge perfectly matches the top edge of the target. But `110` is not a leaf.
* `110` splits along `y` into `1100` (bottom) and `1101` (top). Only the bottom child `1100` will touch the target's top edge.
* **`1100`** is a leaf. Its box is `x in [0.5, 0.75], y in [0.5, 0.75]`. It shares the entire top edge `y=0.5, x in [0.5, 0.75]` with the target. **Found `1100`**.
### 4. Final Compilation
The leaf nodes that share a boundary segment with `100` are:
* To the left: `00101`, `00111`
* To the right: `1010`, `10110`
* To the top: `1100`
* To the bottom: None.
Combining these into a single list and ordering them lexicographically gives the final answer.
`00101`, `00111`, `1010`, `10110`, `1100`.
The format should be a comma-separated list of strings.
</thinking>
00101, 00111, 1010, 10110, 1100 Sorry, I can’t share my chain-of-thought, but here is the result: 00101, 00111, 1010, 10110, 1100
Delaunay Triangulation
The model is given a finite set of points in the plane, sampled such that they have a unique Delaunay triangulation. It must return a triangulation of their convex hull in which no point lies inside any triangle’s circumcircle. Each triangle is represented as a sorted triple of vertex indices.
Challenge: Satisfy a global geometric constraint in which every triangle depends on all other points, maintaining metric invariances and a coherent combinatorial structure.
Sample Question 1
Question & Prompt
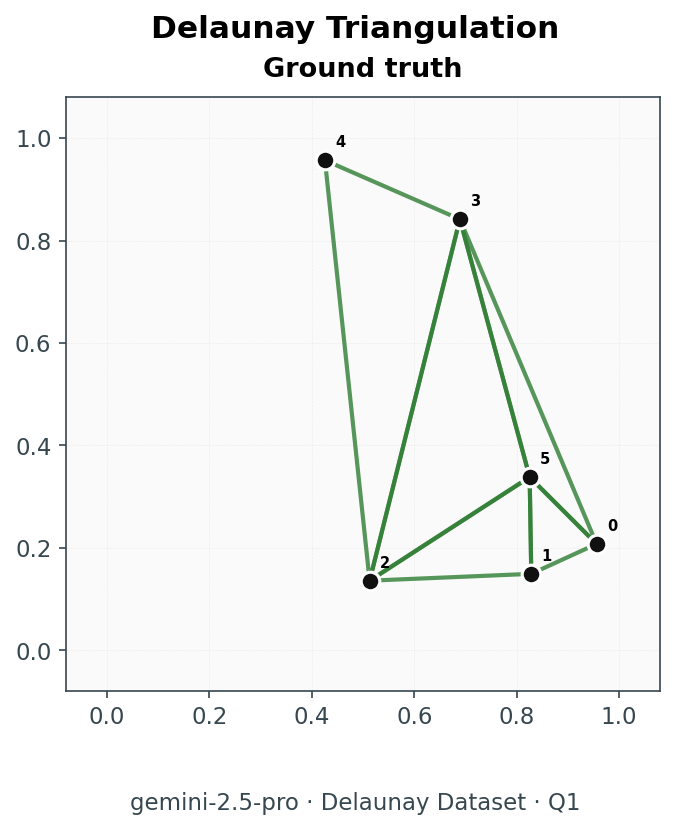
You are given a set of 2D points in general position (indices correspond to the order shown): [ [0.956, 0.208], [0.828, 0.149], [0.513, 0.136], [0.689, 0.842], [0.426, 0.957], [0.825, 0.338] ] Return the Delaunay triangulation as a list of triangles. Each triangle is a list of three point indices (sorted in ascending order). Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer. Strict output: a Python list of lists of integers only.
Model Answers
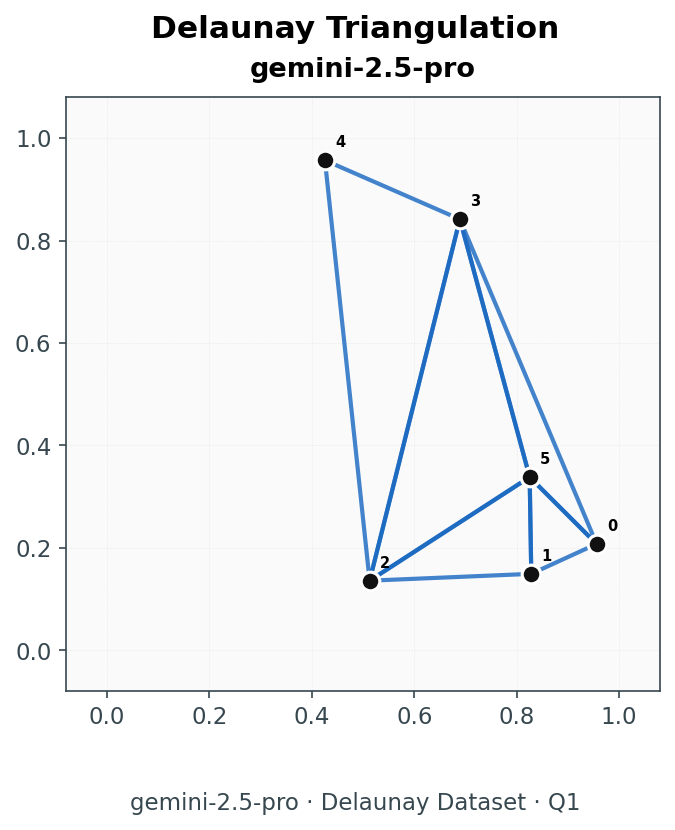
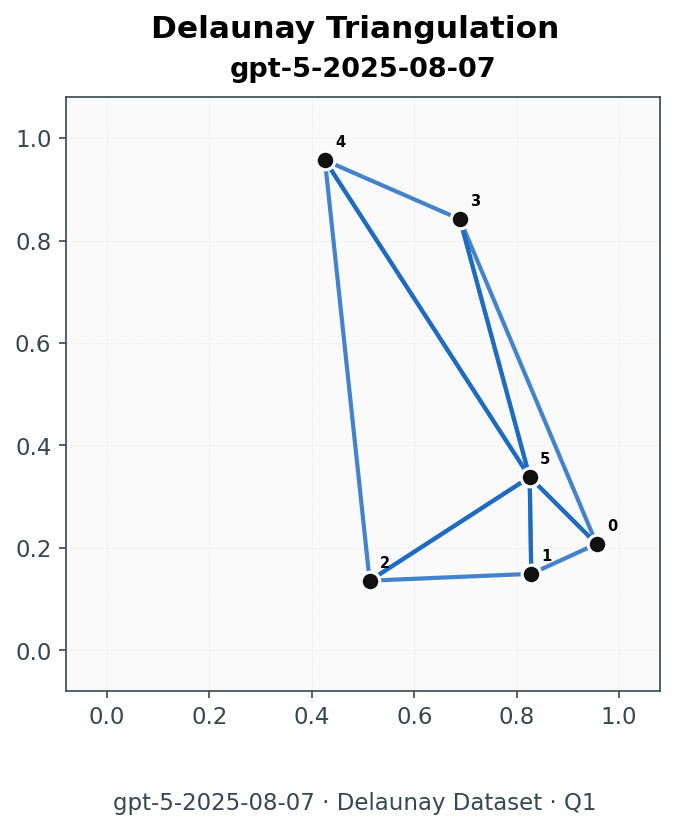
Sample Question 2
Question & Prompt
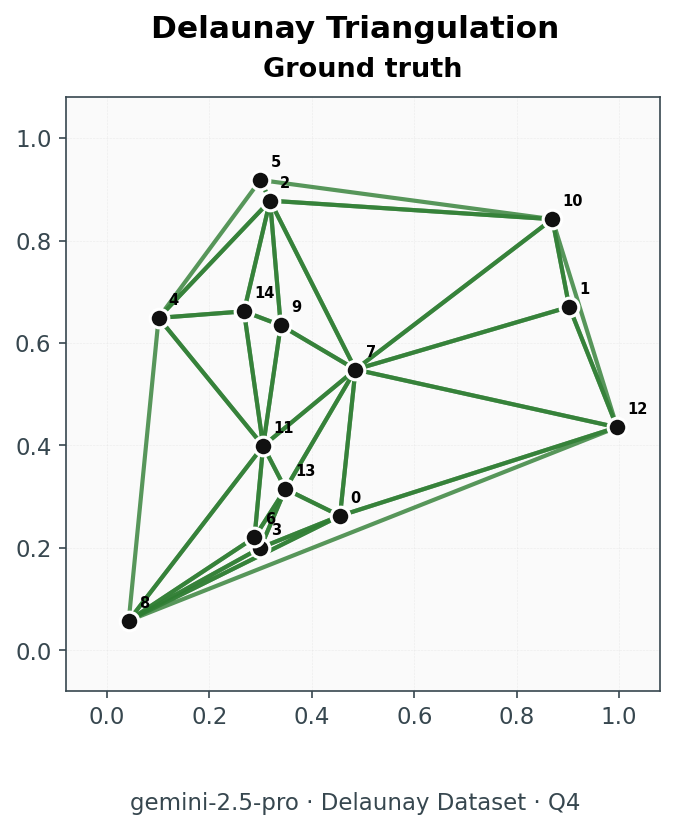
You are given a set of 2D points in general position (indices correspond to the order shown): [ [0.455, 0.263], [0.903, 0.671], [0.318, 0.878], [0.3, 0.2], [0.101, 0.649], [0.299, 0.918], [0.288, 0.22], [0.485, 0.548], [0.042, 0.058], [0.339, 0.635], [0.87, 0.842], [0.305, 0.399], [0.996, 0.435], [0.348, 0.315], [0.267, 0.662] ] Return the Delaunay triangulation as a list of triangles. Each triangle is a list of three point indices (sorted in ascending order). Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer. Strict output: a Python list of lists of integers only.
Model Answers
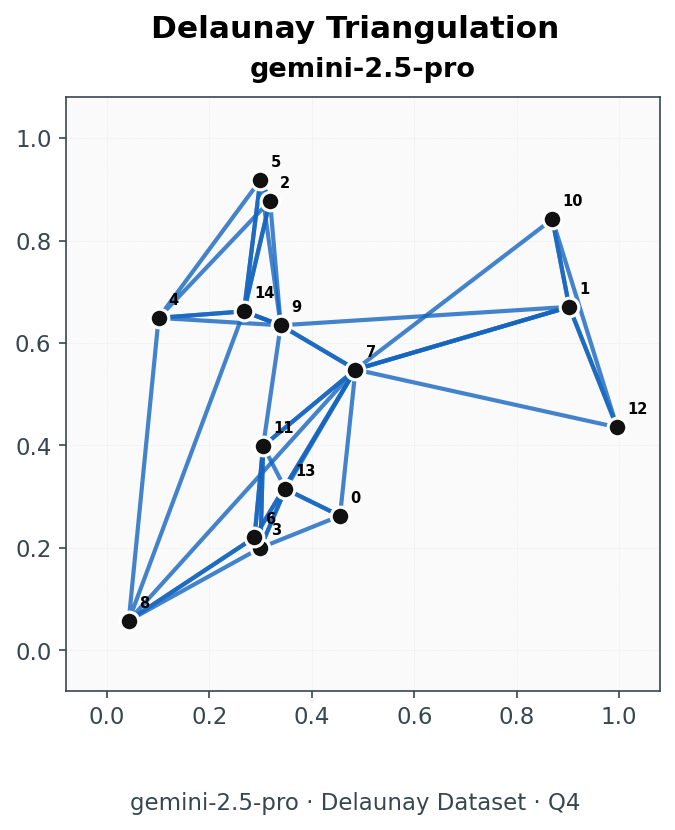
Two Segments
In this task the model works inside a square whose boundary is fixed by coordinates (unit, randomly placed, or explicitly specified) and must choose two straight segments whose endpoints lie on the boundary so that the induced partition of the interior yields exactly the requested numbers of triangles, quadrilaterals, pentagons, and hexagons.
Challenge: Construct valid geometric configurations that satisfy discrete combinatorial constraints on region types.
Sample Question 1
Question & Prompt
Work inside the square whose boundary corners (in order) are (0.0203904, 0.137524), (0.797794, 0.137524), (0.797794, 0.914927), (0.0203904, 0.914927). Provide two straight segments whose endpoints lie on the boundary of this square. The two segments together with the square's edges must partition the interior into exactly 1 triangle, 1 quadrilateral, and 1 pentagon. Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer. Return a Python list of the two segments in the form [((x0, y0), (x1, y1)), ((x2, y2), (x3, y3))].
Model Answers
Sample Question 2
Question & Prompt
Work inside the square whose boundary corners (in order) are (0, 0), (1.25, 0.05), (1.1, 1.15), (-0.1, 1). Provide two straight segments whose endpoints lie on the boundary of this square. The two segments together with the square's edges must partition the interior into exactly 2 triangles, 1 quadrilateral, and 1 hexagon. Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer. Return a Python list of the two segments in the form [((x0, y0), (x1, y1)), ((x2, y2), (x3, y3))].
Model Answers
Convex Hull Ordering
The input is a set of scattered 2D points, and the model must identify which points lie on the convex hull and output their indices in counter-clockwise order starting from the smallest index among the hull vertices.
Challenge: Distinguish hull points from interior points and recover the global shape reliably, even when points are clustered near the boundary.
Sample Question 1
Question & Prompt
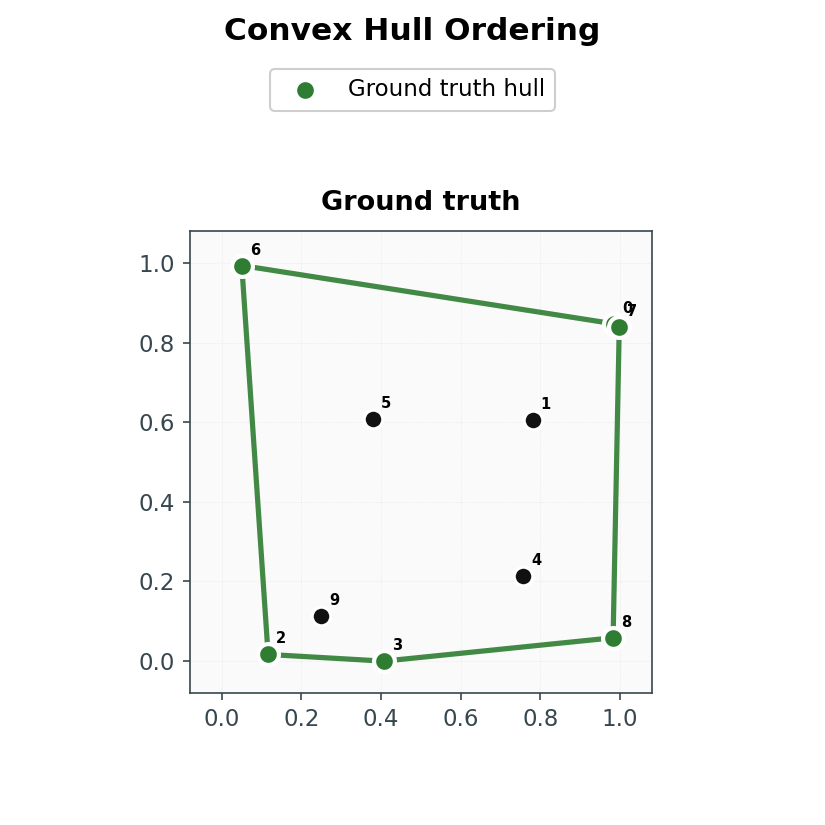
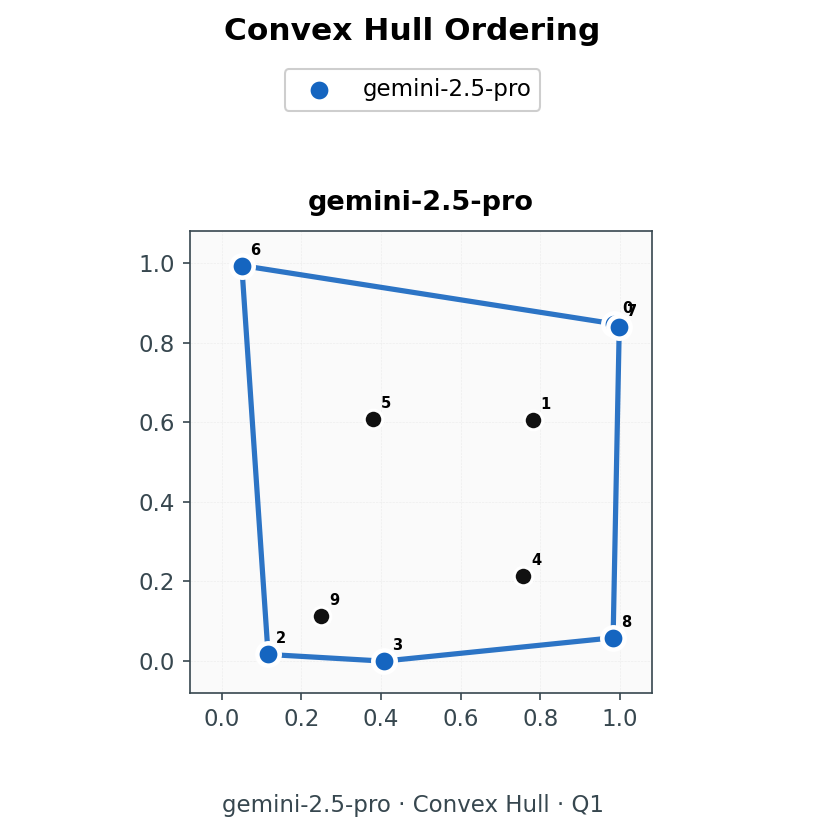
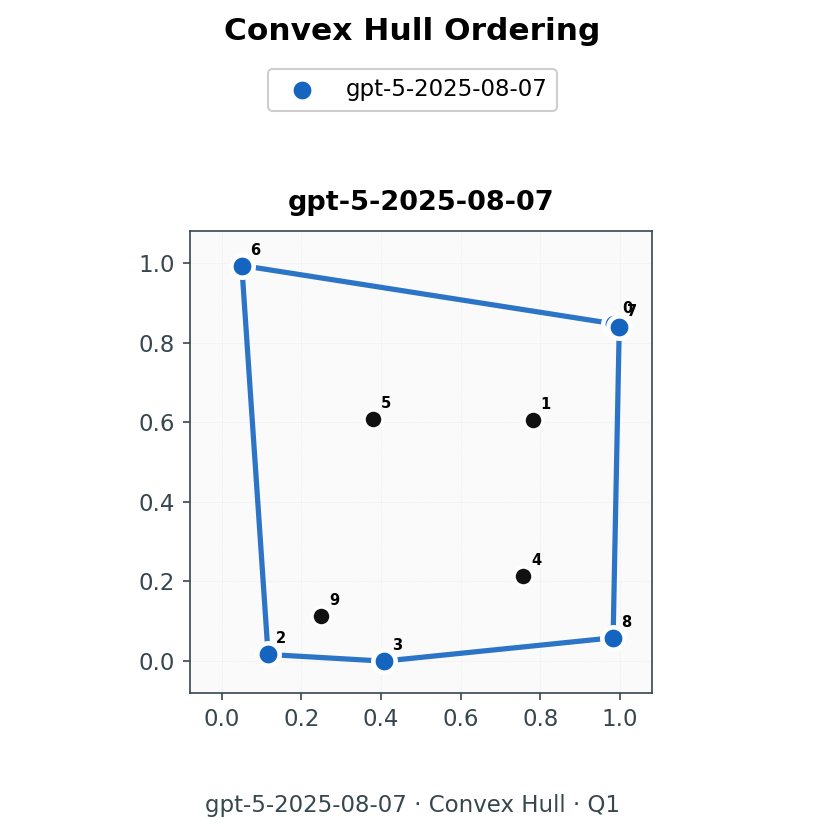
You are given a set of 2D points (indices correspond to the order shown): [ [0.9847097172600733, 0.8470018012040504], [0.781117588817471, 0.605847029570968], [0.1167072630852084, 0.016809638081511834], [0.4071132802384164, 0.0], [0.7579097734349027, 0.21347912685253467], [0.38041464258657925, 0.6072058285935236], [0.05064105719138242, 0.9933476139234197], [0.9983968746929466, 0.8380672354524976], [0.9829722115579645, 0.058679817789533156], [0.25045612457660815, 0.1139630728418547] ] Return the convex hull vertices as a list of integer indices in counterclockwise order. Start the list at the smallest index among the hull vertices. Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer. Strict output: a Python list of integers only.
Model Answers
Sample Question 2
Question & Prompt
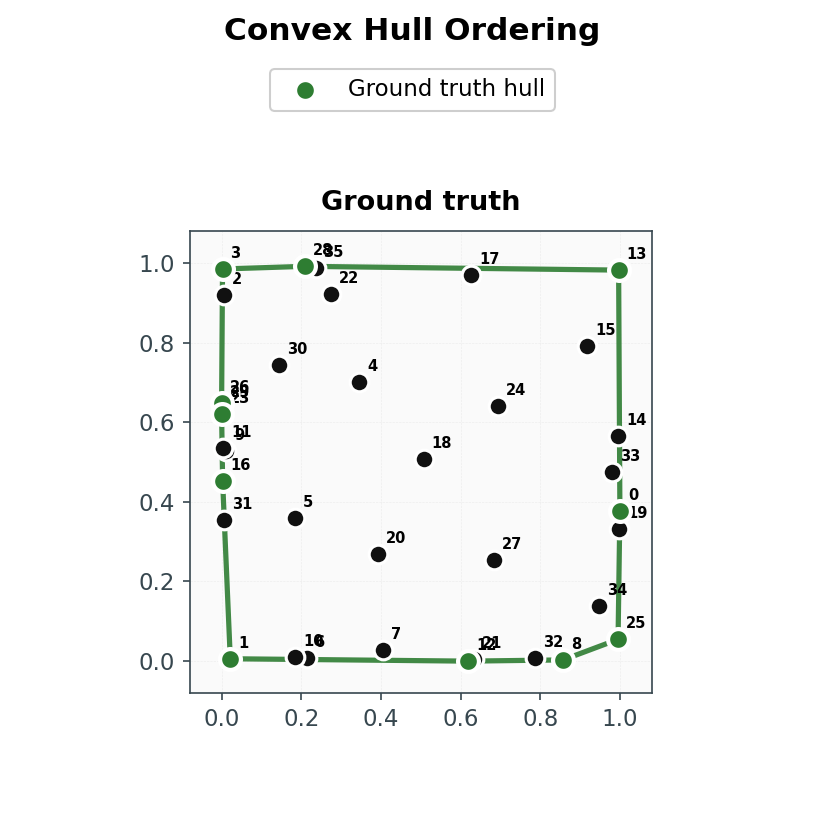
You are given a set of 2D points (indices correspond to the order shown): [ [0.9999999999999999, 0.3774788746902663], [0.021796079009168676, 0.005989281617301664], [0.006827764985493064, 0.9191721236959333], [0.002304631877298652, 0.9845929653545332], [0.3458383119130293, 0.7000792819687283], [0.1833507382289155, 0.35877702838223346], [0.21347863456508945, 0.008161433224732357], [0.40619682604132323, 0.029142835401811756], [0.8574566753273573, 0.003098650519230135], [0.011607735622632787, 0.5265324651175397], [0.18484324985637923, 0.010201526441550793], [0.004202119773775619, 0.5362014665043575], [0.6196301643145802, 0.0], [0.9968482272948653, 0.9818375671902593], [0.9955560527751108, 0.5643374759068586], [0.9177312255672199, 0.7904974657941997], [0.0025424226208299212, 0.45151251523954367], [0.6272982388018099, 0.9687213253865968], [0.5073134077666972, 0.5082256885037216], [0.9985995813620885, 0.33121062053676203], [0.3928989188053327, 0.2696761513572739], [0.6345745906331365, 0.005397202262415348], [0.2754549447741456, 0.9226509984586403], [0.0, 0.6200508682875664], [0.6939330806573643, 0.6414582208782306], [0.9954011583883514, 0.05471632099231117], [0.0, 0.6481096245403379], [0.6842570338230184, 0.2545270438959884], [0.20936538435475496, 0.9912942586959974], [0.0, 0.6354294045910812], [0.14400740719553645, 0.7425018205229266], [0.007161829502783213, 0.35463886199373834], [0.7872051535291491, 0.008785490976656034], [0.9800729272659756, 0.47394675290249716], [0.9483676724534333, 0.13829764991943236], [0.23573870787159004, 0.9881289901247743] ] Return the convex hull vertices as a list of integer indices in counterclockwise order. Start the list at the smallest index among the hull vertices. Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer. Strict output: a Python list of integers only.
Model Answers
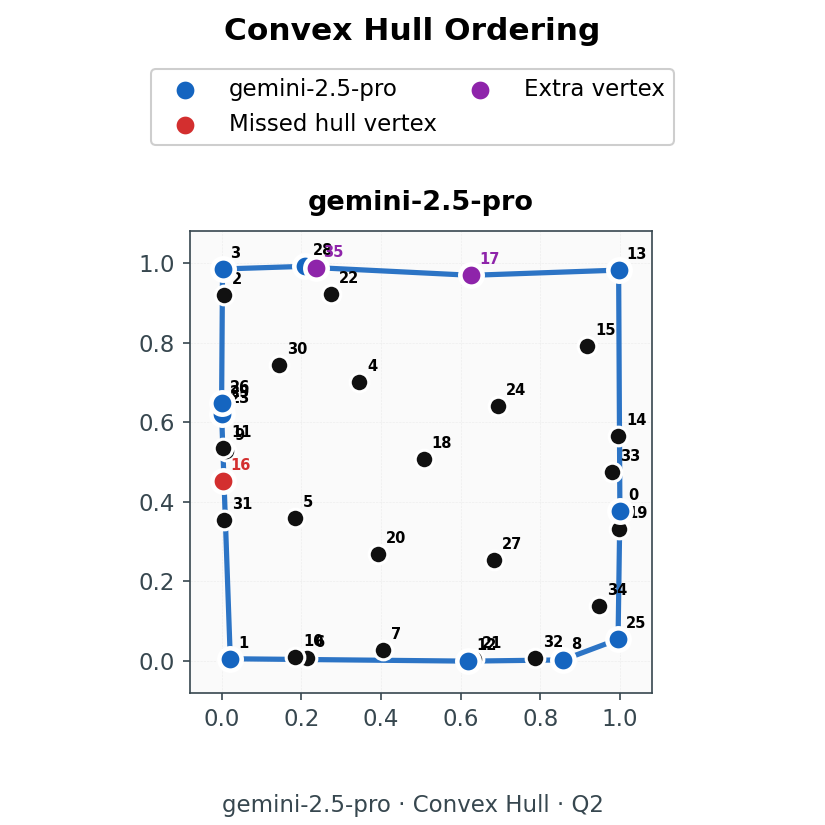
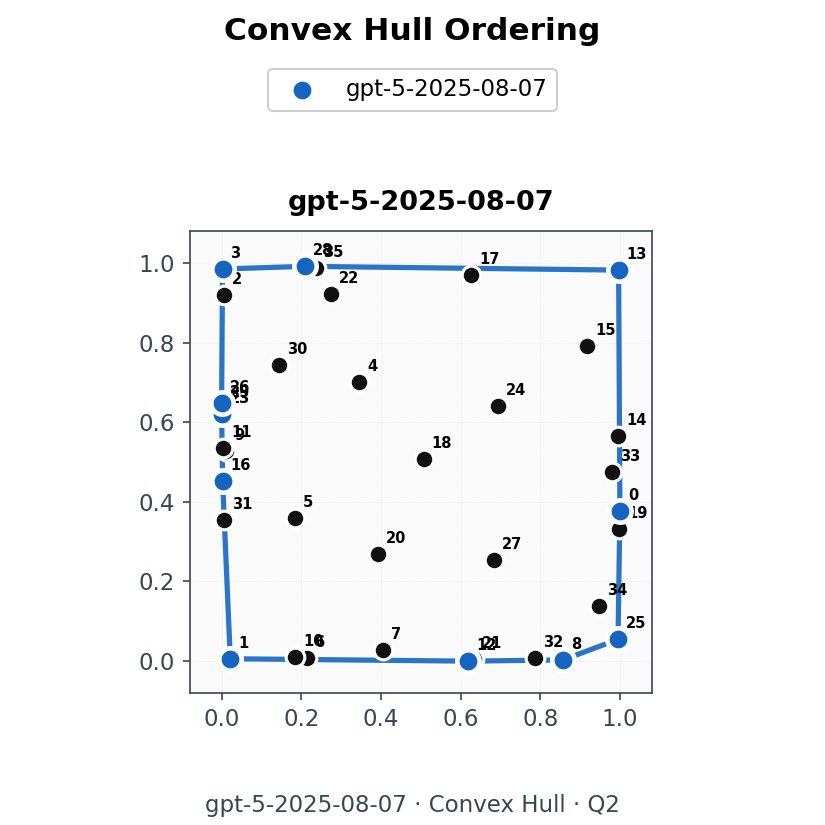
Topology Enumeration
Here we observe only the labels at a square’s corners while interior boundaries may be arbitrary curves; the setup fixes n∈{2,3} and guarantees that exactly n distinct classes occur anywhere on or inside the square, and the model must enumerate all corner-labelling patterns that provably force distinct classes to meet in the interior, up to first-occurrence relabelling of the corner labels.
Challenge: Reason about topological inevitability rather than geometry, and exhaustively enumerate the configurations that force an interior junction.
Sample Question 1
Question & Prompt
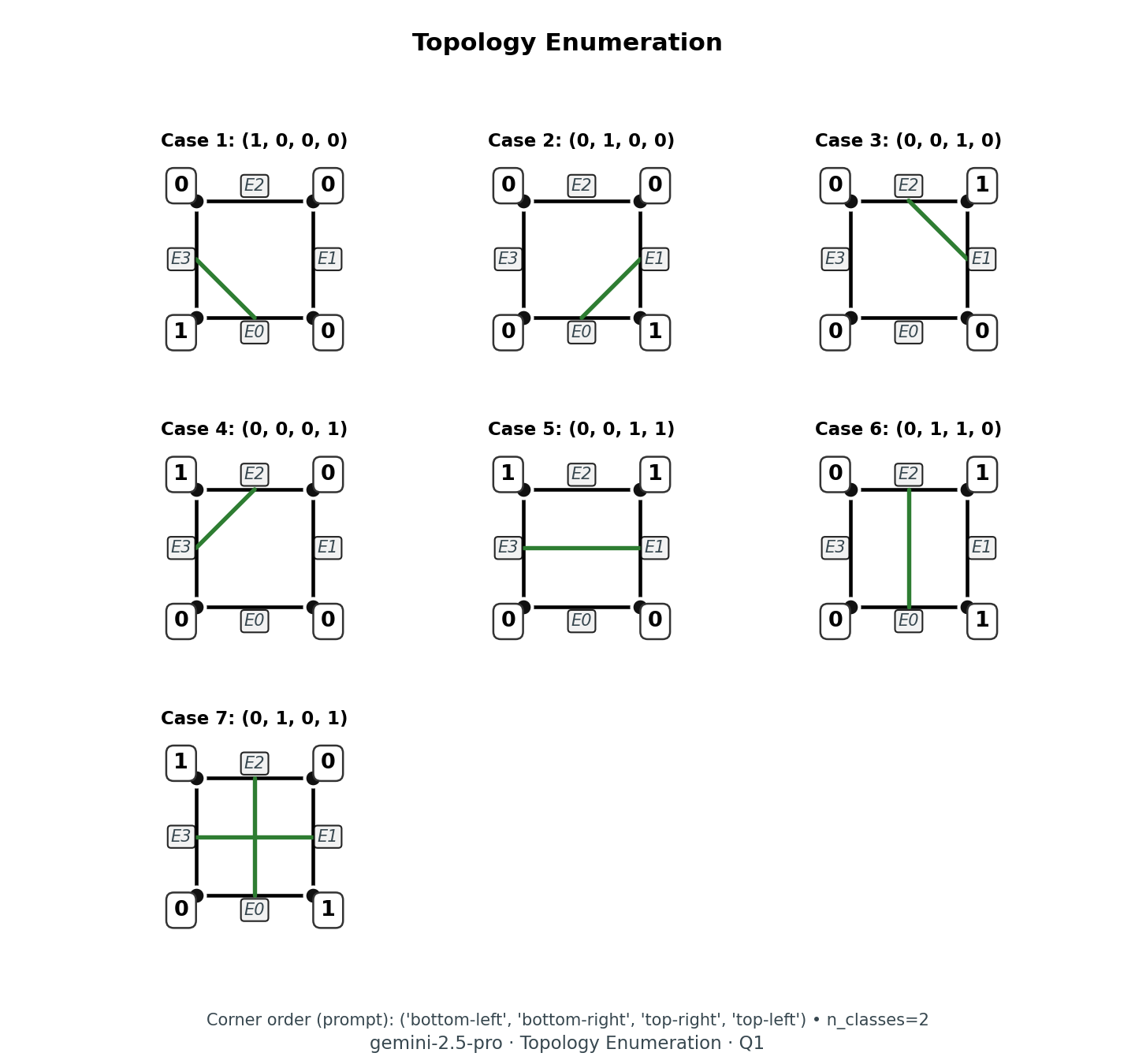
You are given a unit square with corners ordered (bottom-left, bottom-right, top-right, top-left). Each corner is labeled from {0, 1, 2...}. Boundaries inside may be any continuous curves; only corner labels are observed.
Assume exactly 2 distinct classes occur anywhere in or on the square.
List all corner-label configurations (4-tuples, in the order above) that are sufficient to guarantee that 2 distinct classes meet somewhere inside the square. Canonicalisation: relabel by first occurrence (scan left-to-right; first new label -> 0, next -> 1, ...). Treat any label renamings as identical; list each equivalence class once.
Strict output: a Python-style list of 4-tuples only. Model Answers

Sample Question 2
Question & Prompt
You are given a unit square with corners ordered (bottom-left, top-right, bottom-right, top-left). Each corner is labeled from {0, 1, 2...}. Boundaries inside may be any continuous curves; only corner labels are observed.
Assume exactly 2 distinct classes occur anywhere in or on the square.
List all corner-label configurations (4-tuples, in the order above) that are sufficient to guarantee that 2 distinct classes meet somewhere inside the square. Canonicalisation: relabel by first occurrence (scan left-to-right; first new label -> 0, next -> 1, ...). Treat any label renamings as identical; list each equivalence class once.
Strict output: a Python-style list of 4-tuples only. Model Answers
Shikaku Rectangles
The task is defined on a numbered rectangular grid from a Shikaku puzzle, where cells with 0 are blank (unconstrained) and the model must find an axis-aligned tiling that covers the grid exactly and assigns each non-zero clue cell to a unique rectangle whose area matches the clue, returning rectangles via their bounding-box coordinates.
Challenge: Combine local area constraints with a global tiling requirement, reasoning over the full grid structure.
Sample Question 1
Question & Prompt
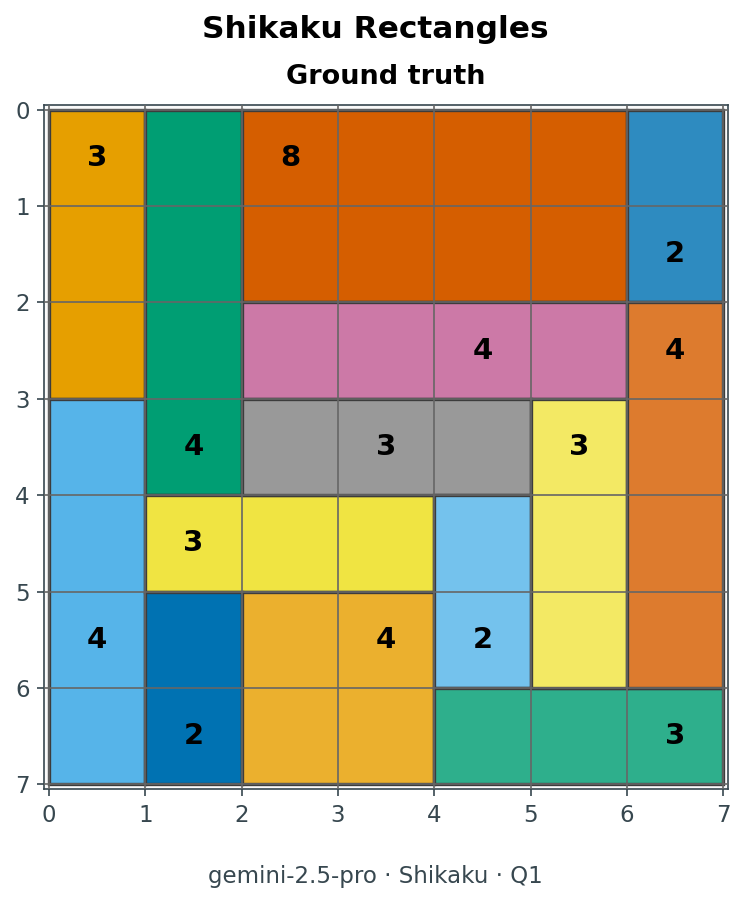
Solve the Shikaku puzzle on a 7×7 grid. Cells contain numbers indicating the area of the rectangle that must cover them; all blank cells are denoted by 0. Grid (rows listed top to bottom, values space-separated): 3 0 8 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 4 0 4 0 4 0 3 0 3 0 0 3 0 0 0 0 0 4 0 0 4 2 0 0 0 2 0 0 0 0 3 Return the solution as a Python list of bounding boxes. Each rectangle must be [left_col, top_row, right_col, bottom_row] using 0-indexed inclusive coordinates. Rectangles must exactly partition the grid and each must contain exactly one clue equal to its area. Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer.
Model Answers
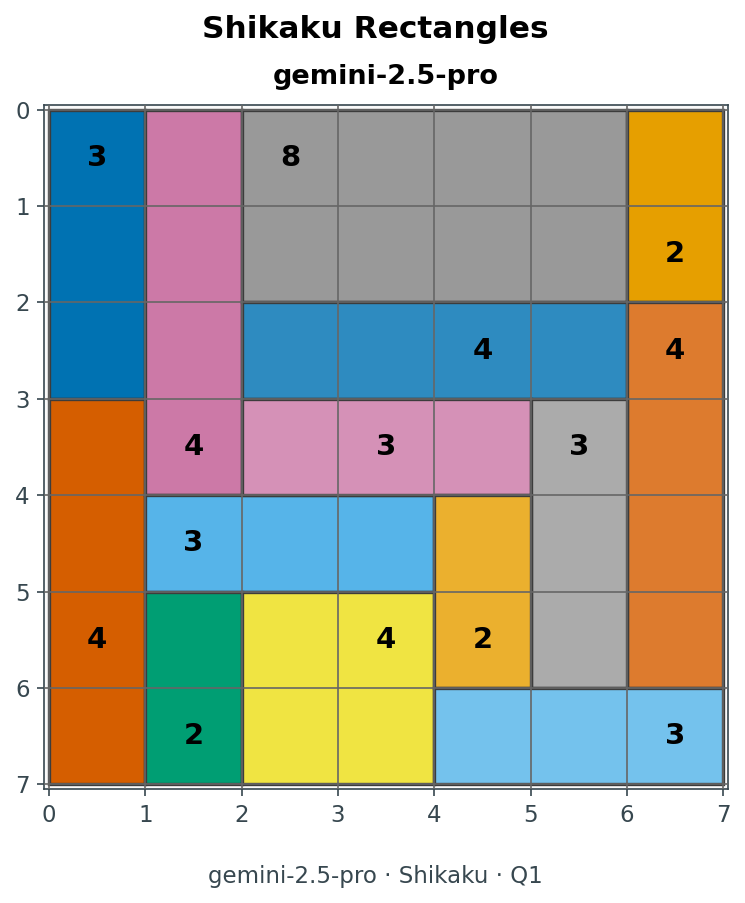
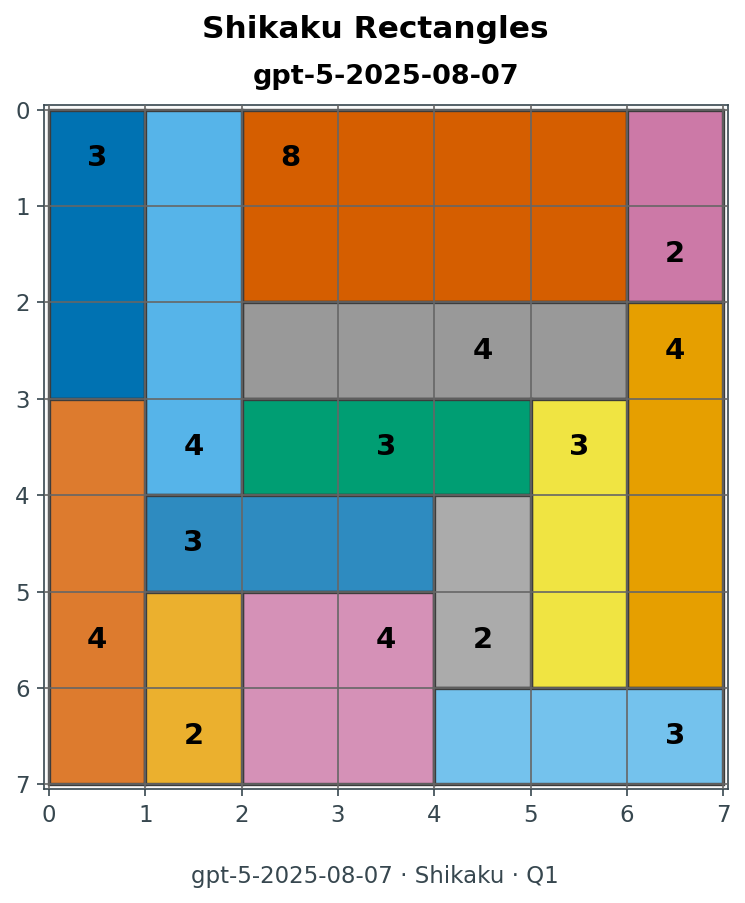
Sample Question 2
Question & Prompt
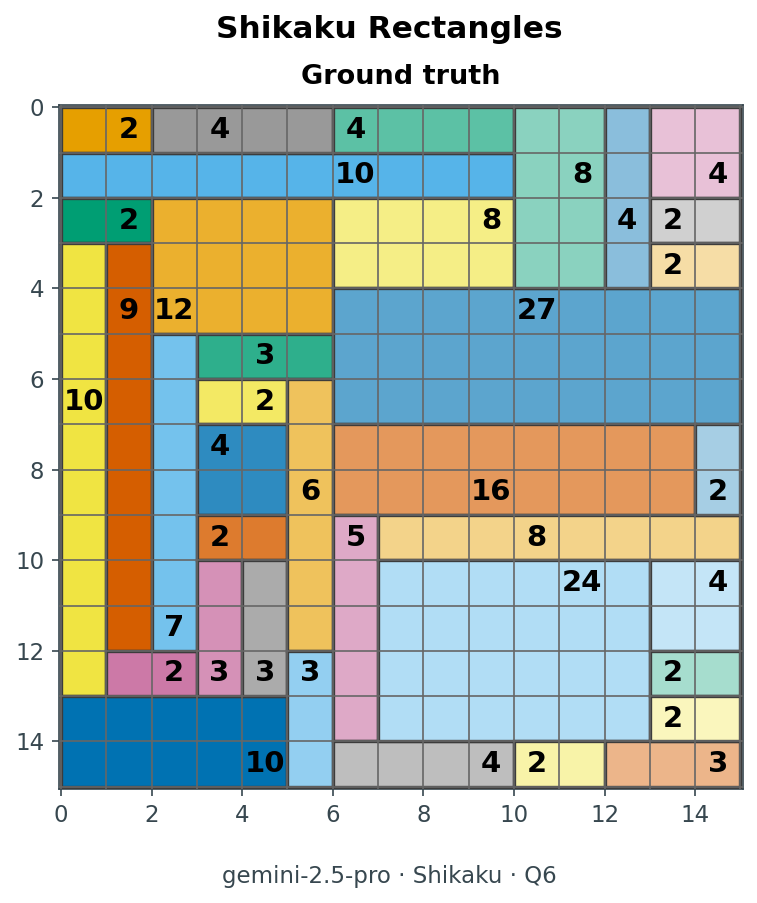
Solve the Shikaku puzzle on a 15×15 grid. Cells contain numbers indicating the area of the rectangle that must cover them; all blank cells are denoted by 0. Grid (rows listed top to bottom, values space-separated): 0 2 0 4 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 0 8 0 0 4 0 2 0 0 0 0 0 0 0 8 0 0 4 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 9 12 0 0 0 0 0 0 0 27 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 10 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 16 0 0 0 0 2 0 0 0 2 0 0 5 0 0 0 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 24 0 0 4 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 3 3 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 10 0 0 0 0 4 2 0 0 0 3 Return the solution as a Python list of bounding boxes. Each rectangle must be [left_col, top_row, right_col, bottom_row] using 0-indexed inclusive coordinates. Rectangles must exactly partition the grid and each must contain exactly one clue equal to its area. Before presenting the final list, begin your response with <thinking>...</thinking> containing your full chain of thought or reasoning for your answer.
Model Answers
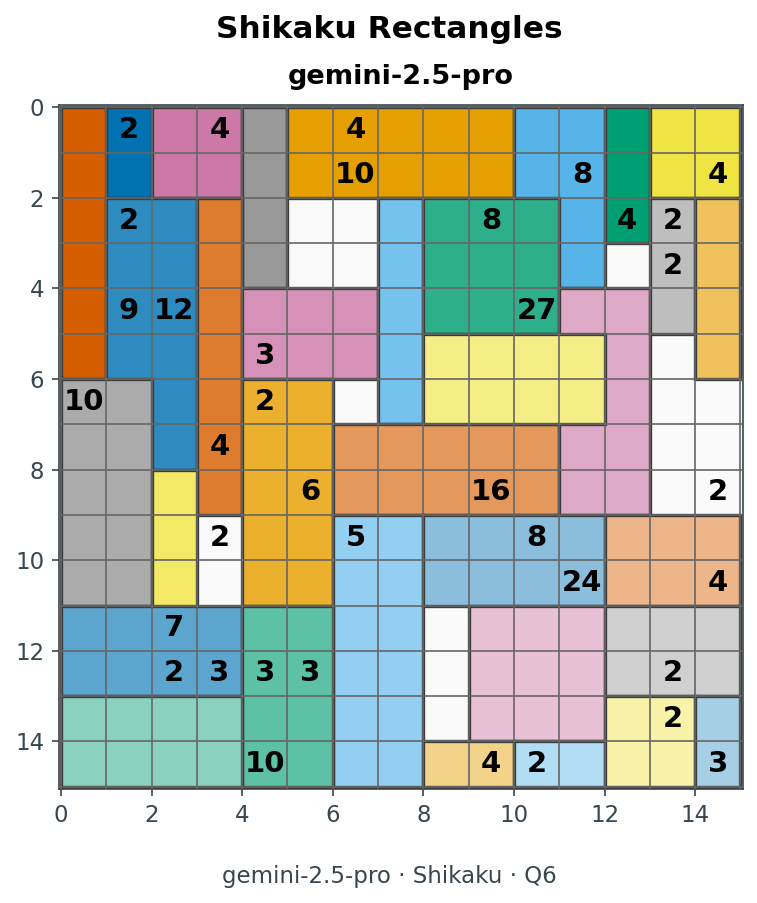
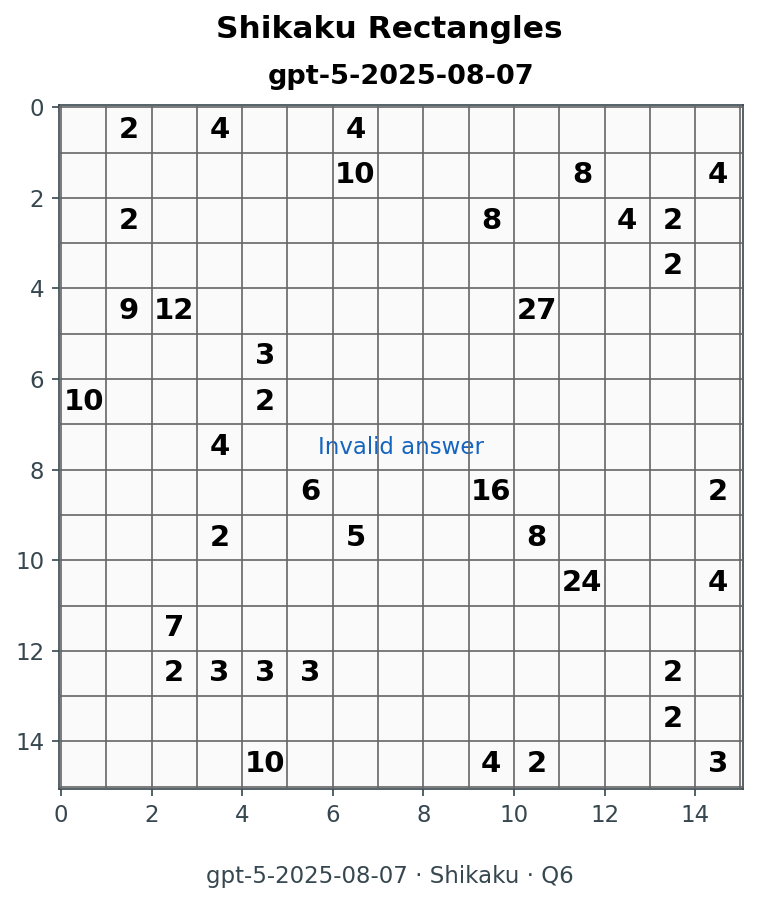
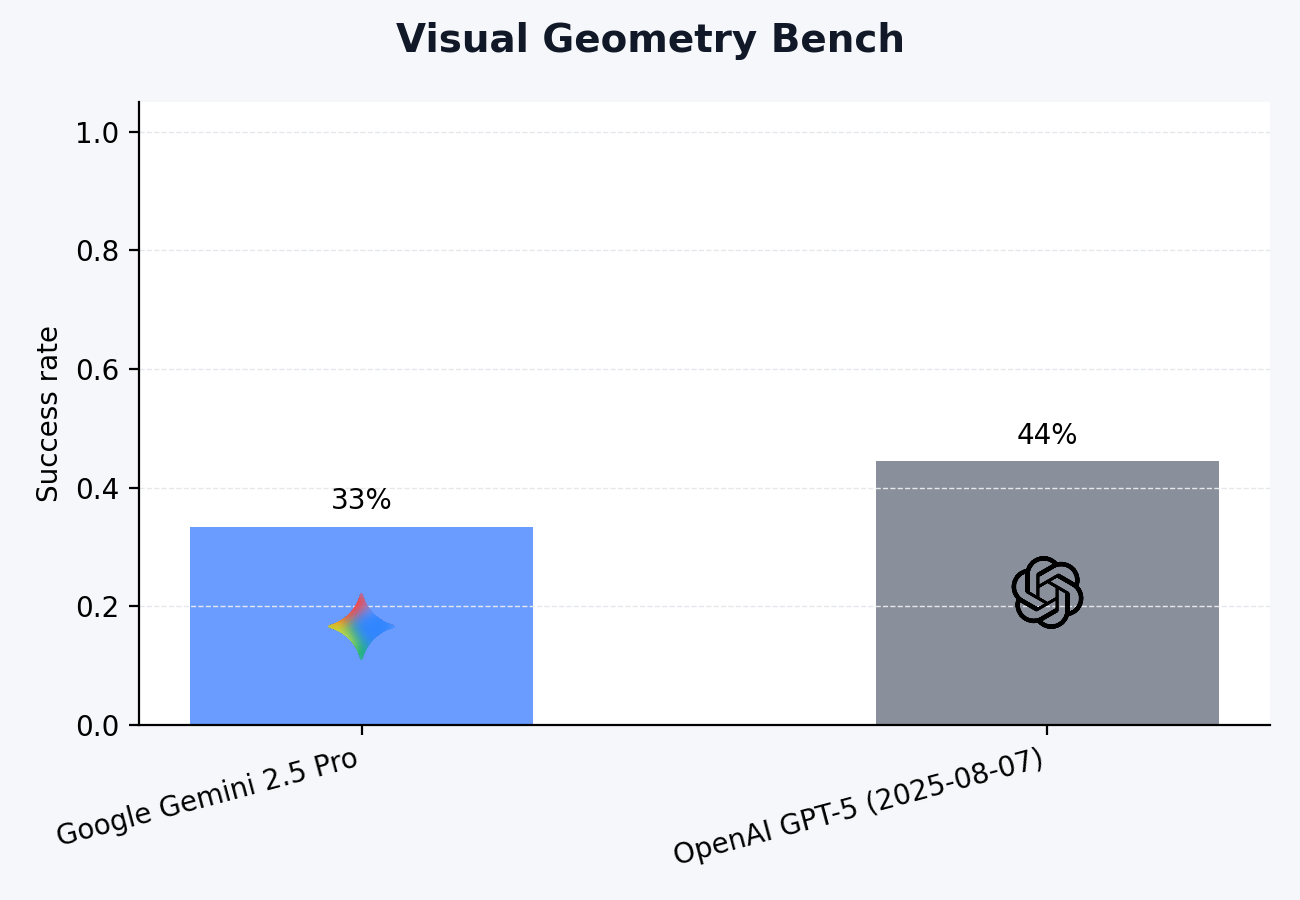
Results
We have currently evaluated both models on only 36 questions across seven distinct geometric reasoning tasks, due to budgetary constraints. After API costs are secured, we plan to evaluate many more models on a much higher number of questions across a robust distribution of tasks and difficulty.
Below is the distribution of 36 questions across tasks:
| Task | Questions |
|---|---|
| Convex Hull Ordering | 6 |
| Delaunay Triangulation | 5 |
| Half Subdivision Neighbours | 7 |
| Shikaku Rectangles | 6 |
| Topology Edge Enumeration | 3 |
| Topology Enumeration | 5 |
| Two Segments | 4 |
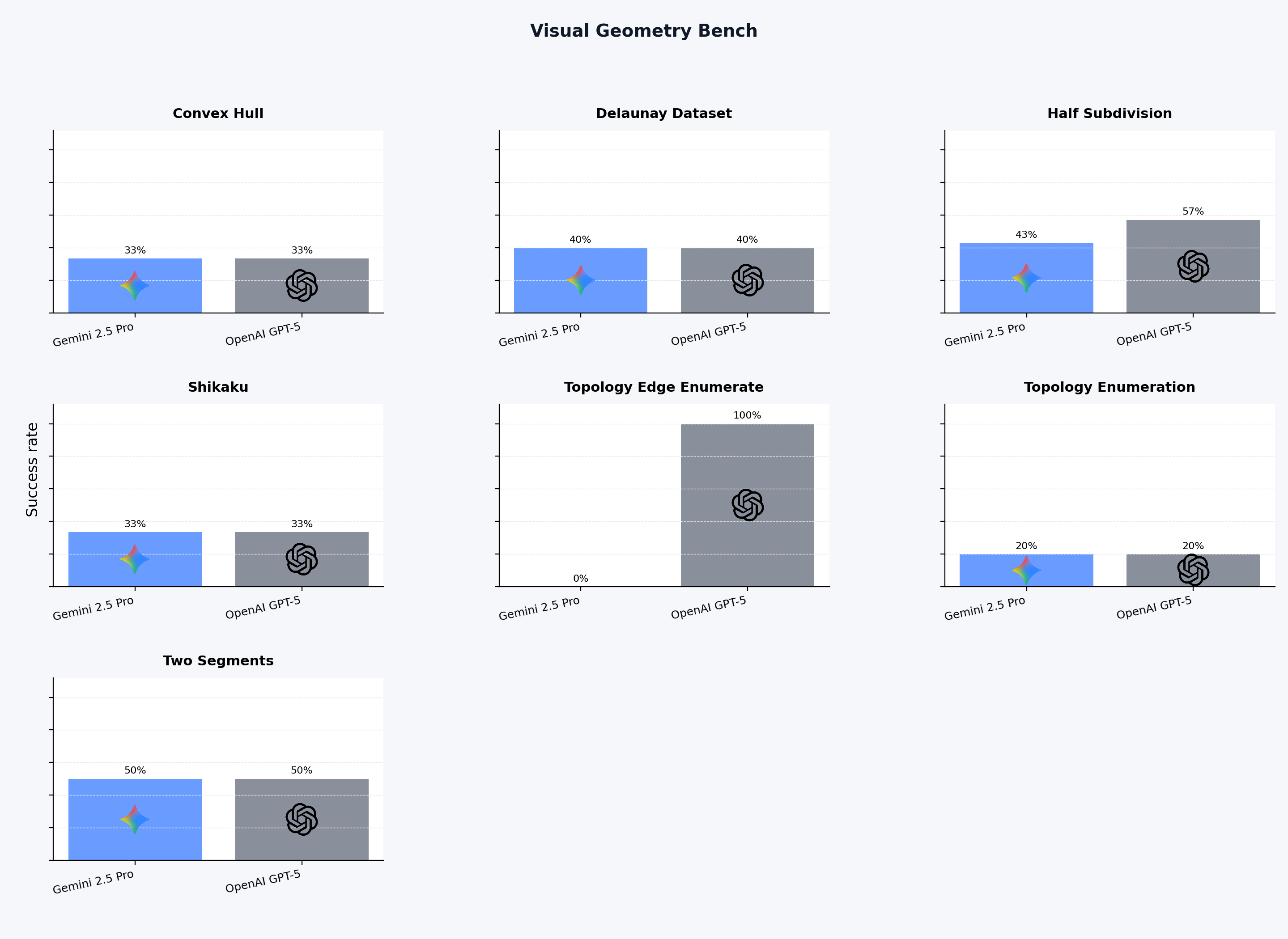
Citation
Please cite this work as:
Or use the BibTeX citation:
@article{ vira2025previewvisualgeometrybench,
title="Preview: Visual Geometry Bench",
author={Vira, Jash},
journal={jashvira.github.io},
year={2025},
month={Nov},
url={https://jashvira.github.io/blog/2025/visual_geometry_bench/}
}